


Next: Symmetric group algebra
Up: Symmetric group
Previous: Symmetric group
The symmetric group
(SG )
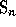 of degree n is the group of the
of degree n is the group of the
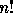 permutations (
permutations (ListPerm )
of the set 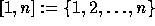 . It is defined for any
n>0 and given a m>n, we have
. It is defined for any
n>0 and given a m>n, we have 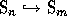 since we can
identify
since we can
identify 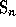 with the subgroup of
with the subgroup of 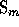 by adding to any
permutation
by adding to any
permutation 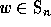 the fixed points
the fixed points 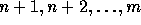 . Using this embedding,
we define the group
. Using this embedding,
we define the group 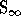 of all permutations of the set of positive
integers that fix all but a finite number of them:
of all permutations of the set of positive
integers that fix all but a finite number of them:

We usually denote a permutation 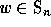 by the list of the images of
by the list of the images of
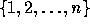 under w, seen as a mapping of
under w, seen as a mapping of 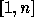 onto itself:
onto itself:
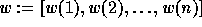 .
.
A basic statistic on
permutations is the notion of inversion: given a permutation 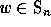 ,
an inversion is defined to be a couple
,
an inversion is defined to be a couple 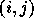 of indices
such that
of indices
such that 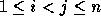 and
and 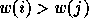 . We will refer to an inversion
on consecutive positions i and i+1 as a descent
(
. We will refer to an inversion
on consecutive positions i and i+1 as a descent
(Perm2Desc )
of the permutation and
conversely, we will talk about a rise of a given permutation w as a
position i such that 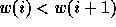 .
.
The length 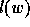 (
(Perm2Length )
of a given permutation w is the number of
inversions of w, i.e. the cardinal of the set 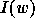 (
(Inversions )
of inversions of w:
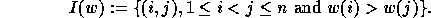
The element 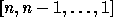 of
of 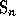 is called the maximal
permutation
(
is called the maximal
permutation
(LastPerm )
of 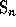 because
it has the maximal number of inversions for the symmetric group of
degree n, i.e. the binomial
because
it has the maximal number of inversions for the symmetric group of
degree n, i.e. the binomial 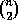 .
.
The notion of inversion leads to another coding of the
elements of the symmetric group.
Given a permutation 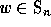 , we define the code
, we define the code 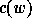 (
(Perm2Code )
to be a vector of
non-negative integers, the i-th component being the number of positions j>i
such that 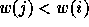 .
One can
check that the length of the permutation w is the sum of all
components of the code
.
One can
check that the length of the permutation w is the sum of all
components of the code 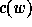 . The code
. The code 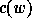 of the permutation
of the permutation
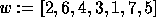 is
is 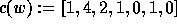 .
.
Given a permutation 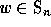 , we can fill a
, we can fill a 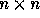 square matrix
with 0's and 1's so that the sub-matrix of
1's exactly represents the permutation w: this is done by having a 1
in all positions
square matrix
with 0's and 1's so that the sub-matrix of
1's exactly represents the permutation w: this is done by having a 1
in all positions 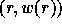 for
for 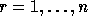 where r denotes a row
index and
where r denotes a row
index and 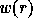 stands for a column index. All other values being set
to 0. For instance, we show the
stands for a column index. All other values being set
to 0. For instance, we show the 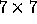 square matrix representing the
permutation
square matrix representing the
permutation 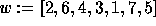 ,
,

In a quite similar manner, we introduce the diagram 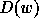 of a permutation
of a permutation
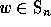 . This combinatorial object is defined to be a
. This combinatorial object is defined to be a
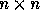 square matrix filled as follows: we put a circle
square matrix filled as follows: we put a circle  at position (r, c) where r (respectively c) is a row index (resp.
column index) whenever there is an inversion
at position (r, c) where r (respectively c) is a row index (resp.
column index) whenever there is an inversion 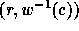 in which
in which
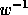 denotes the inverse permutation of w. Consider the element of
denotes the inverse permutation of w. Consider the element of 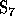 ,
say
,
say 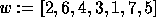 , its diagram
, its diagram 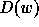 is the following:
is the following:

since there is an inversion between the first position (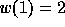 )
and the value 1, between the second position (
)
and the value 1, between the second position (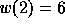 ) and the values
1,3,4 and 5 (second row of the previous diagram), and so on.
The code of a permutation w can also be defined as the sequence of numbers
of circles in the successive rows of the diagram
) and the values
1,3,4 and 5 (second row of the previous diagram), and so on.
The code of a permutation w can also be defined as the sequence of numbers
of circles in the successive rows of the diagram 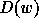 .
.
Let 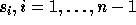 be the elementary transposition that interchanges
i and i+1, and fixes all other values. In other words,
be the elementary transposition that interchanges
i and i+1, and fixes all other values. In other words,
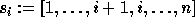 where i+1 lies at position i,
or equivalently
where i+1 lies at position i,
or equivalently
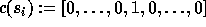 in which the unique 1 lies at
position i.
Elementary transpositions satisfy the following relations:
in which the unique 1 lies at
position i.
Elementary transpositions satisfy the following relations:
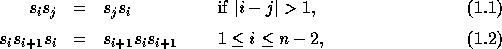
known as braid relations, together with the extra relation:

this last relation being changed into more general quadratic relations
to get the different Hecke algebras (NCA, IDCA, HEKA, HEQA).
We constantly use the decomposition of a permutation as a product of simple
transpositions, product of minimal length, reduced decomposition
(Perm2Rd ).
This decomposition is far from being unique
(ListRd ): the number of reduced
decompositions is given by the function NbRd .
Let us fix the convention used to multiply a permutation w by an
elementary transposition 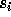 :
:
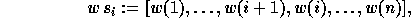
where 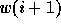 lies at position i, and
lies at position i, and
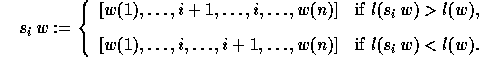
One can easily compute a reduced decomposition of a
permutation w from its diagram.
Reading the diagram 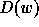 from left to right and top to bottom, we replace each circle
by a positive integer i starting from the row number, and increasing
the value of i by 1 at each step. It gives a canonical reduced
decomposition of the corresponding permutation by reading this
Rothe diagram from right to left and downwards, each i being
interpreted as the elementary transposition
from left to right and top to bottom, we replace each circle
by a positive integer i starting from the row number, and increasing
the value of i by 1 at each step. It gives a canonical reduced
decomposition of the corresponding permutation by reading this
Rothe diagram from right to left and downwards, each i being
interpreted as the elementary transposition 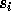 exchanging i and i+1. Given a permutation
exchanging i and i+1. Given a permutation 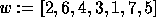 , its
Rothe diagram is
, its
Rothe diagram is

from which we deduce a reduced decomposition of w, that is
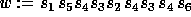 .
.
The set of reduced decompositions ranked according to their lengths, with
edges corresponding to simple transpositions, is called the
permutohedron, the order being the weak order: this is
the natural order for divided differences
(NCA ).
To the permutohedron, one can add edges between permutations which differ
by a transposition and with lengths differing by 1. The order is now called
the Bruhat order, and is the natural order for the idCoxeter algebra
(IDCA ).
The interval of permutations below a given one is obtained with the function
Interval ;
Betti(perm) gives the number
of permutations in the interval corresponding to the permutation perm according
to their lengths.



Next: Symmetric group algebra
Up: Symmetric group
Previous: Symmetric group
 of degree n is the group of the
of degree n is the group of the
 permutations (
permutations (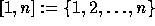 . It is defined for any
n>0 and given a m>n, we have
. It is defined for any
n>0 and given a m>n, we have 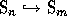 since we can
identify
since we can
identify 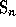 with the subgroup of
with the subgroup of 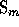 by adding to any
permutation
by adding to any
permutation 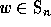 the fixed points
the fixed points 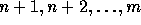 . Using this embedding,
we define the group
. Using this embedding,
we define the group 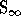 of all permutations of the set of positive
integers that fix all but a finite number of them:
of all permutations of the set of positive
integers that fix all but a finite number of them:




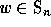 by the list of the images of
by the list of the images of
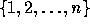 under w, seen as a mapping of
under w, seen as a mapping of 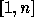 onto itself:
onto itself:
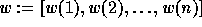 .
.
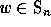 ,
an inversion is defined to be a couple
,
an inversion is defined to be a couple 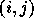 of indices
such that
of indices
such that 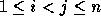 and
and 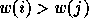 . We will refer to an inversion
on consecutive positions i and i+1 as a descent
(
. We will refer to an inversion
on consecutive positions i and i+1 as a descent
(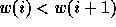 .
.
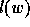 (
(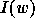 (
(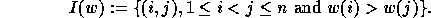
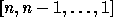 of
of 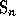 is called the maximal
permutation
(
is called the maximal
permutation
(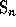 because
it has the maximal number of inversions for the symmetric group of
degree n, i.e. the binomial
because
it has the maximal number of inversions for the symmetric group of
degree n, i.e. the binomial 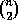 .
.
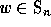 , we define the code
, we define the code 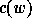 (
(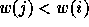 .
One can
check that the length of the permutation w is the sum of all
components of the code
.
One can
check that the length of the permutation w is the sum of all
components of the code 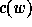 . The code
. The code 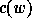 of the permutation
of the permutation
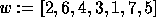 is
is 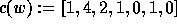 .
.
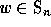 , we can fill a
, we can fill a 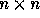 square matrix
with 0's and 1's so that the sub-matrix of
1's exactly represents the permutation w: this is done by having a 1
in all positions
square matrix
with 0's and 1's so that the sub-matrix of
1's exactly represents the permutation w: this is done by having a 1
in all positions 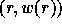 for
for 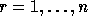 where r denotes a row
index and
where r denotes a row
index and 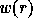 stands for a column index. All other values being set
to 0. For instance, we show the
stands for a column index. All other values being set
to 0. For instance, we show the 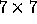 square matrix representing the
permutation
square matrix representing the
permutation 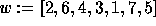 ,
,

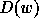 of a permutation
of a permutation
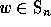 . This combinatorial object is defined to be a
. This combinatorial object is defined to be a
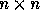 square matrix filled as follows: we put a circle
square matrix filled as follows: we put a circle  at position (r, c) where r (respectively c) is a row index (resp.
column index) whenever there is an inversion
at position (r, c) where r (respectively c) is a row index (resp.
column index) whenever there is an inversion 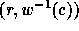 in which
in which
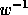 denotes the inverse permutation of w. Consider the element of
denotes the inverse permutation of w. Consider the element of 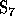 ,
say
,
say 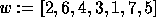 , its diagram
, its diagram 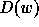 is the following:
is the following:

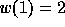 )
and the value 1, between the second position (
)
and the value 1, between the second position (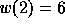 ) and the values
1,3,4 and 5 (second row of the previous diagram), and so on.
The code of a permutation w can also be defined as the sequence of numbers
of circles in the successive rows of the diagram
) and the values
1,3,4 and 5 (second row of the previous diagram), and so on.
The code of a permutation w can also be defined as the sequence of numbers
of circles in the successive rows of the diagram 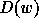 .
.
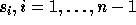 be the elementary transposition that interchanges
i and i+1, and fixes all other values. In other words,
be the elementary transposition that interchanges
i and i+1, and fixes all other values. In other words,
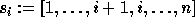 where i+1 lies at position i,
or equivalently
where i+1 lies at position i,
or equivalently
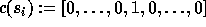 in which the unique 1 lies at
position i.
Elementary transpositions satisfy the following relations:
in which the unique 1 lies at
position i.
Elementary transpositions satisfy the following relations:
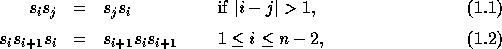

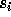 :
:
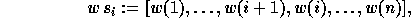
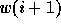 lies at position i, and
lies at position i, and
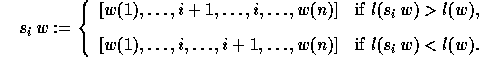
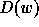 from left to right and top to bottom, we replace each circle
by a positive integer i starting from the row number, and increasing
the value of i by 1 at each step. It gives a canonical reduced
decomposition of the corresponding permutation by reading this
Rothe diagram from right to left and downwards, each i being
interpreted as the elementary transposition
from left to right and top to bottom, we replace each circle
by a positive integer i starting from the row number, and increasing
the value of i by 1 at each step. It gives a canonical reduced
decomposition of the corresponding permutation by reading this
Rothe diagram from right to left and downwards, each i being
interpreted as the elementary transposition 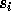 exchanging i and i+1. Given a permutation
exchanging i and i+1. Given a permutation 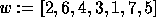 , its
Rothe diagram is
, its
Rothe diagram is

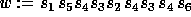 .
.