
UNIVERSITE PARIS VII
THESE DE DOCTORAT
SPECIALITE : INFORMATIQUE FONDAMENTALE
PRESENTE PAR Dominique REVUZ
DICTIONNAIRES ET LEXIQUES
METHODES ET ALGORITHMES
SOUTENUE LE 22 Février devant la commission d'examen
JURY
Mr Maxime CROCHEMORE, (rapporteur)
Mr Maurice GROSS , (président)
Mr Gaston GROSS
Mr Dominique PERRIN
Mr Jean Marie RIFFLET
Mr Jean Marc STEYAERT
Les dictionnaires électroniques des langues naturelles sont des outils fondamentaux pour l'analyse ou la génération automatique de textes en langue naturelle. Ils sont utilisés dans les correcteurs orthographiques, les phonétiseurs ou les traducteurs automatiques.
La présente thèse expose les possibilités qu'offrent les automates acycliques pour représenter les lexiques. La représentation par automates acycliques est économique en espace, elle permet de réaliser une compression importante des données. Elle fournit également des fonctions d'accès et de recherche de motifs, des plus rapides.
Un de nos résultats les plus intéressants est la création d'un algorithme de minimisation des automates acycliques en temps linéaire, qui rend raisonnable le coût des mises à jour du lexique, si on veut garder l'automate minimal.
L'utilisation des automates acycliques est limitée aux lexiques, qui sont de simples listes de mots, ou à des dictionnaires dans lesquels le nombre d'informations associées aux mots est faible. Un dictionnaire de ce type peut être représenté par un automate à multi-terminaux : contenant plusieurs ensembles d'états terminaux. Un tel automate fournit l'information associée à un mot en fonction de l'ensemble terminal atteint. Si on veut avoir accès à une information différente pour chaque mot, une autre représentation est nécessaire, les automates à multi-terminaux devenant des arbres de trop grande taille.
Nous proposons pour ces dictionnaires complexes un hybride des arbres lexicographiques et des automates qui conjugue les avantages des deux structures : l'automate représentant la liste de mots et l'arbre permettant un hachage performant.
Nous exposons une méthode simple pour transformer un automate en transducteur de hachage. La fonction réalisée par ce transducteur est une fonction de hachage parfaite : on a un seul élément par adresse et toutes les adresses sont utilisées. Nous montrons la faisabilité et l'efficacité pratique de cette fonction de hachage.
Le principe de transformation d'un automate en transducteur, qui s'effectue sans changer le graphe sous-jacent, est appliqué pour créer un compresseur de textes écrits en langue naturelle. Les résultats expérimentaux de compression apportent un nouvel élément dans la détermination de l'entropie des textes en langue naturelle. Il sont plus efficaces que tous les algorithmes de compression classiques appliqués à la langue naturelle.
Pour représenter un dictionnaire phonétique nous avons mis au point un algorithme de construction d'un transducteur à partir d'une transduction définie par une liste de couples. Nous avons ensuite cherché à offrir une réponse pratique et ponctuelle au problème de la minimisation des transducteurs, en utilisant les caractéristiques de la transduction à représenter.
Nous présentons un nouveau modèle de transducteur, dit transducteur à retour, qui représente mieux la transduction empirique, ce qui permet de proposer une phonétisation de bonne qualité des mots inconnus. Un autre apport de ce nouveau type de transducteur est de pouvoir être minimisé (comme peut l'être un automate) de façon efficace.
Toute analyse de texte passe par une première phase d'analyse lexicale. Cette analyse consiste à tester l'appartenance de chaque mot du texte à un lexique c'est à dire à la simple liste des mots de la langue, en général on cherche à extraire les informations associées à chacun de ces mots dans le dictionnaire de la langue. Ces informations sont généralement constituées de la partie du discours, d'une définition au sens usuel des dictionnaires, ou encore d'informations grammaticales concernant le mot et ses contextes. Les deux fonctions de test et d'extraction doivent être optimisées pour rendre les programmes d'analyse suffisamment rapides.
Pour éviter les échecs de consultation et pour améliorer les procédures d'analyse lexicale de très grands dictionnaires ont été construits. Des problèmes de stockage et de manipulation se posent du fait de leur grande taille, nos recherches portent sur ces problèmes.
Une façon d'aborder les problèmes de taille peut être d'utiliser des méthodes de compression de données. Mais en règle générale les algorithmes de compression mettent les données sous une forme non utilisable par les fonctions d'accès. Les méthodes de compression classiques sont de plus délicates à utiliser : si un bit est perdu le dictionnaire entier peut être perdu. L'utilisation d'automates nous a paru séduisante. Elle offrait a priori de nombreux avantages : fonctions d'accès accélérées par rapport aux autres méthodes, compression excellente, et robustesse correcte.
Dans la première partie les dictionnaires et lexiques sur lesquels nous effectuons notre étude sont décrits. Nous présenterons dans la deuxième partie quelques-unes des méthodes classiques utilisées pour manipuler les dictionnaires. La troisième partie est consacrée aux automates, qui constituent un mode de représentation important des lexiques. Un nouvel algorithme de minimisation est présenté.
La quatrième partie concerne les transducteurs et les nombreuses possibilités qu'ils offrent pour la description de dictionnaires ou de grammaires: les dictionnaires phonétiques mis sous forme de transducteurs et de transducteur à retour ; un outil pour la représentation des dictionnaires complexes, en utilisant les transducteurs comme fonction de hachage ( un dictionnaire complexe est un dictionnaire dans lequel une information différente est associée a chaque mot). La cinquième partie est consacrée aux transducteurs définis sur un automate. Ces transducteurs nous permettent de créer des compresseurs de textes en langue naturelle. Plusieurs algorithmes sont présentés pour mettre en oeuvre ces compresseurs. L'algorithme de minimisation des automates acycliques est décrit dans la sixième partie. Pour conclure nous présenterons quelques options choisies pour notre corpus de dictionnaires.
Les annexes contiennent des mises en oeuvre en langage C des algorithmes présentés, ainsi que des valeurs expérimentales obtenues pour diverses représentations des dictionnaires par automates ; nous donnons également des résultats sur différents tests de compression effectués sur un corpus de textes en français.
La variable T représente la taille du dictionnaire (ou du lexique) sous forme de texte, mesurée en octets ou mots-mémoire, clefs et données comprises dans le cas des dictionnaires, ou clefs seulement dans le cas des lexiques.
Le rapport R représente le rapport de compression existant entre la taille T du dictionnaire sous forme de texte, et la taille T' de sa représentation obtenue par nos différentes méthodes soit :
R=F(T';T)
ce rapport doit être inférieur à 1 pour qu'il y ait compression.
La variable n représente le nombre d'entrées du dictionnaire (ou du lexique).
La fonction logarithme en base b est notée logb().
Nous utilisons pour parler de complexité des algorithmes la notation O(f(n)). On dit d'une fonction g(n) qu'elle est d'une complexité en O(f(n)) si
il existe c il existe N0 tel que quelque soit n > N0 g(n)<=c.f(n), où c et N sont des constantes.
la variable n doit mesuré de façon pertinente la taille de l'entrée (des données) d'un algorithme.
Exemple :
La recopie du dictionnaire sous forme de texte est une opération linéaire qui dépend de la taille du dictionnaire. Sa complexité est donc de O(T). En pratique cette opération n'est malheureusement pas linéaire.
Nous utiliserons comme unité de stockage le Méga octet, noté Mo,soit 220 octets ou caractères, exactement 1.048.576 octets .
Exemple :
aile,N21
où N21 indique un nom féminin qui prend un s au pluriel.
Le DELAS utilise environ 500 codes distincts, on peut donc considérer que notre donnée associée est un entier de l'intervalle [1,...,500].
Le DELAS utilise 2Mo d'espace de stockage sous forme de fichier texte.
Nous présentons page suivante Figure 1. un extrait de ce dictionnaire.
Figure 1.
autojustification,.N21
autojustifier,.V3
autolanceur,.A1
autolimitation,.N21
autolimiter,.V3
autolubrifiant,.A32
autolubrification,.N21
autolubrifier,.V3
autolustrant,.N1.A32
autolysat,.N1
autolyse,.N21
autolyser,.V3
automasser,.V3
automate,.N1.N31
automaticien,.N41
automaticité,.N21
automation,.N21
automatique,.N1.N21.A31
automatiquement,.ADVE
automatisation,.N21
automatiser,.V3
automatisme,.N1
automédication,.N21
automédiquer,.V3
automédon,.N1
automitrailler,.V3
automitrailleuse,.N21
automnal,.A76
automne,.N1
Les codes .A76 .N1 N1.N21.A31 sont en pratique transfomés en codes numériques comme dans l'exemple de la Figure 3.
Exemple :
prenne, prendre,V66:S3s:S1s
prendre verbe de type 66, au subjonctif présent, 3e et 1ère personnes du singulier.
On en donne un fragment figure 2.
Le DELAF utilise moins de 8.500 codes différents, on peut donc considérer que notre donnée associée est un entier de l'intervalle [1,..., 8.500].
Le DELAF occupe 12Mo d'espace de stockage sous forme de fichier texte, le seul lexique du DELAF utilisant 6,7Mo.
Nous présentons figure 3. un extrait de ce dictionnaire dans un format ayant subi une compression. Les quatre lettres qui suivent un symbole % constituent un préfixe commun à tous les mots suivants, jusqu'au prochain symbole %. Les numéros qui précèdent éventuellement une virgule codent les 1000 suffixes les plus fréquents. Les numéros qui suivent la virgule indicent les codes du dictionnaire. Cette représentation permet de réduire l'espace de stockage à 5 Mo, mais elle ralentit les fonctions d'accès.
Figure 2.
Figure 3.
%auto,741
accusa,29
acc800,8
accusa1,23
accu25,27
accu24,22
accus14,5
accu23,36
acc801,30
accus11,25
accusas2,21
accusa9,26
accusas3,19
accusass0,20
acc804,4
accus12,6
accusa78,450
accusat21,470
accusa20,2
accusat0,3
Exemple :
un cordon bleu et un cordon orange
Le premier est considéré comme un mot composé : un cordon bleu peut être un être humain, une personne qui fait bien la cuisine, ce mot composé a donc un sens en plus du sens calculable : un cordon de couleur bleue. Le deuxième est une séquence libre de mots simples et désigne un cordon de couleur orange.
Formellement une entrée du DELAC est une suite de mots simples, accompagnée d'une information sur la partie du discours et d'une information sur la flexion. En général, les codes utilisés dans le DELAC sont les mêmes que ceux utilisés dans le DELAF.
Exemple :
achat:N1/à//terme,un:Nms
associé à : un achat à terme, nom masculin singulier
le code du DELAS N1 permet la mise au pluriel :
achats/à//terme,des:Nmp
adjoint:N32/à/le/maire,un:Nms
un adjoint au maire, nom masculin singulier.
le code N32 permet la mise au féminin et au pluriel.
adjointe/à/le/maire,une:Nfs
une adjointe au maire, nom féminin singulier.
adjoints/à/le/maire,des:Nmp
adjointes/à/le/maire,des:Nfp
Il existe un DELACF, où les mots composés sont sous forme fléchie.
Exemple :
phonémique,fonemik,.A31
phonétiquement,fonetik'mant*,.ADVE
La clef est le mot, et la donnée sa phonémisation suivie de l'information du DELAS sur la partie du discours. Dans ce dictionnaire une donnée différente est associée à chaque mot, ce qui le distingue des deux précédents dictionnaires. Le DELAP est un dictionnaire complexe, c'est à dire où chaque clef est associée a une donnée différente.
Il existe un DELAPF, où les mots phonémisés sont sous forme fléchie.
Nous présentons figure 4. un extrait de ce dictionnaire.
Figure 4.
phone,fon,.N1
phonématique,fonematik,.N21.A31
phonématiquement,fonematik'mant*,.ADVE
phonème,fonem,.N1
phonémique,fonemik,.A31
phonémiquement,fonemik'mant*,.ADVE
phonéticien,fonetisien*,.N41-32
phonétique,fonetik,.N21.A31
phonétiquement,fonetik'mant*,.ADVE
phonétisation,fonetizasion*,.N21
phonétiser,fonetize,.V3
phonétisme,fonetism,.N1
phoniatre,foniatr,.N31
phoniatrie,foniatri,.N21
phonie,foni,.N21
phonique,fonik,.A31
phoniquement,fonik'mant*,.ADVE
phono,fono,.N1
phonocardiographie,fonokardiografi,.N21
phonocinétique,fonosinetik,.A31
phonogénie,fonoZeni,.N21
phonogénique,fonoZenik,.A31
phonogramme,fonogram,.N1
phonographe,fonograf,.N1
phonographique,fonografik,.A31
Les lexiques-grammaires peuvent être assimilés à des listes de formes de phrases possibles. Ces listes de formes sont équivalentes à des listes de mots, et acceptent donc les mêmes types de structures de données que les lexiques. La construction d'algorithmes et leur expérimentation portant sur les dictionnaires se poursuivra sur ces lexiques grammaires.
Figure 5.
Nous lierons le problème de la représentation d'ensembles à celui des fonctions dont nous voulons disposer, soit les trois opérateurs :
- Membre(X,w) : cette fonction a une réponse booléenne indiquant si l'élément w appartient ou non à l'ensemble X ;
- Insérer(X,w) : cette fonction ajoute l'élément w à l'ensemble X, la définition d'ensemble ici étant bien vérifiée, puisque si w appartient déjà à X il n'est pas ajouté ;
- Supprimer(X,w) : élimine de X l'élément w.
Un ensemble munis de ces trois opérateurs et d'un ordre total est appelé dictionnaire (lexique si il n'y a pas de donnée associée).
Pour la représentation d'ensembles d'autres fonctions sont utilisées, comme Union(X,Y), Intersection(X,Y), Minimum(X), Différence(X,Y). Mais ces opérateurs ne sont pas fondamentaux pour notre problème spécifique, et peuvent être construits à partir des trois opérateurs de base.
Nous considérons le lexique du DELAF, c'est à dire uniquement les clefs. Dans les exemples suivants des entiers seront utilisés comme clefs sans perte de généralité.
Nous présentons trois méthodes pour représenter et utiliser les ensembles, les listes, les arbres et le hachage. Elles permettent de représenter indifféremment lexiques ou dictionnaires. Ces méthodes sont théoriquement valables mais la taille de nos dictionnaires les rendent inutilisables en pratique.
Dans une section spéciale nous parlons de méthodes avec bruit et en particulier du codage surimposé qui ne traite que le cas des lexiques, et ce de façon statistique.
Sur ordinateur, les listes sont mises en oeuvre grâce à des tableaux, des pointeurs, ou encore par listes doublement chaînées (un pointeur sur le suivant, et sur le précédent dans la liste). L'utilisation de tableaux permet d'utiliser une fonction Membre à caractère dichotomique.
Ces deux propriétés permettent d'effectuer la maintenance du dictionnaire (adjonctions, suppressions et corrections) et d'extraire facilement des portions de dictionnaires pour l'édition ou le traitement, et ceci en utilisant des applications très simples et déjà existantes.
Les fonctions Insérer(X,w) et Supprimer(X,w) ont une complexité en temps proportionnelle à T.
La fonction Membre(X,w) est coûteuse en temps, même quand on utilise des méthodes rapides comme la recherche dichotomique dont la complexité est de O(log2(n)). Le nombre d'opérations à effectuer est une fonction asymptotique de log2(n), où n est le nombre d'entrées. La dichotomie est pourtant très rapide quand elle est appliquée par un humain qui, lui, a une représentation intuitive de la répartition des mots dans le dictionnaire et va directement à la bonne lettre.
L'espace mémoire nécessaire inclut un (ou deux) pointeur(s) pour chaque entrée, en plus de l'entrée elle même. Le rapport de compression R est supérieur à 1 c'est à dire que cette représentation utilise plus de mémoire que le dictionnaire sous forme de texte.
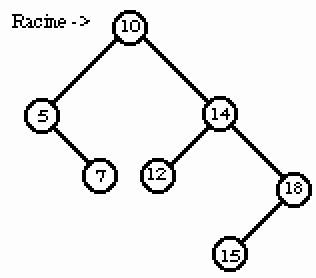
La propriété fondamentale des arbres binaires de recherche est la suivante : pour tous les noeuds, le fils gauche et ses descendants ont tous des clefs inférieures au noeud courant ; et le fils droit et tous ses descendants ont tous des clefs supérieures au noeud courant.
Figure 6. Un arbre binaire de recherche.


La Figure 6. représente un arbre de racine o(O;10) ;
le noeud o(O;14) a pour père o(O;10), et a deux fils o(O;12) et o(O;18) .
le noeud o(O;14) est de hauteur 2.
La complexité en moyenne est une estimation de la complexité, calculée grâce à une estimation probabiliste de la répartition des données.
Les fonctions Insérer(X,w) et Supprimer(X,w) ont une complexité en moyenne de O(log2(n)) où n est le nombre d'éléments de X. Cette complexité peut atteindre O(n) dans le cas le plus défavorable.
Les données peuvent être gardées sous forme de listes, notre arbre contient alors uniquement des pointeurs sur les entrées.
Chaque noeud d'un arbre 2-3 contient deux clefs dont les valeurs respectives sont : la clef minimale des descendants du deuxième fils, et celle des descendants des noeuds du troisième fils. Soit par exemple sur l'arbre de la figure 7. la racine de l'arbre contient 7 et 16 qui sont respectivement le minimum du sous-arbre central et le minimum du sous-arbre de droite. La racine de ce sous-arbre de droite contient une seule valeur : 19 car ce noeud n'a que deux sous-arbres.
Figure 7. Un arbre 2-3.
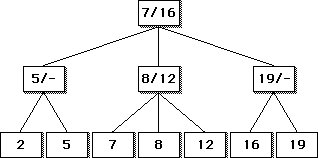
Figure 8. Un arbre lexicographique généralisé.
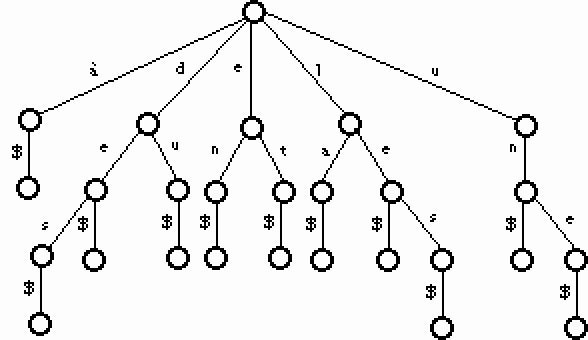
Le DELAF sous forme d'arbre lexicographique généralisé (ALG) utilise 2,08 106 noeuds. Sa taille est de l'ordre de 16Mo. Si nous ajoutons les codes, sa taille atteint environ 24Mo.
Nous insistons sur le fait que par "mémoire centrale", nous entendons "mémoire réelle", et non pas "mémoire virtuelle", laquelle utilise les disques durs pour simuler une augmentation de la taille de la mémoire vive. Dans les calculs de complexité nous ne considérerons donc pas la notion de mémoire virtuelle.
Le temps d'accès aux sous-ensembles est constant. Le temps de calcul de la fonction de hachage est constant. Si la fonction de hachage a été bien choisie, autrement dit si on a peu de mots dans chaque sous-ensemble, l'accès à l'élément recherché dans les sous-ensembles est rapide. On obtient donc globalement un accès rapide à un élément de l'ensemble.
Considérons par exemple la fonction de hachage suivante :
h(w)= L'entier constitué des quatre premières lettres du mot w puisqu'une suite de quatre octets peut indifféremment représenter 4 caractères ou un entier.
Cet entier constitue une adresse à laquelle figurent les mots du dictionnaire qui commençant par ces quatre même lettres. Si le mot a moins de 4 caractères la fonction reste définie. Cette méthode n'est pas injective mais permet de travailler sur des listes de mots beaucoup plus petites que le dictionnaire entier. L'accès par une méthode simple dans ces listes de mots commençant par les mêmes 4 lettres est rapide. Globalement l'accès est accéléré.
Exemple :
L'alphacode est une fonction qui consiste à réécrire les lettres du mot dans l'ordre alphabétique, chacune suivie de son nombre d'occurrences.
alphacode(aimablement )=a2be2ilm2nt
le mot comporte
deux a, un seul b, deux e ...etc
Cette fonction alphacode() est un exemple de bonne fonction pour la dispersion : elle crée peu de collisions, id est, peu de mots ont le même alphacode. Le plus grand sous-ensemble de mots ayant le même alphacode comporte 17 mots dans le cas du DELAF.
Cette approche serait satisfaisante si la table d'adressage n'était pas énorme : le rapport de compression R est supérieur à 10.
L'espace occupé dans les mémoires de masse est également fortement augmenté, soit par la nécessité d'utiliser des fichiers structurés, soit du fait de la multiplication du nombre de fichiers nécessaires. Trouver une bonne fonction de hachage dans le cas de clefs de taille variable reste un problème ouvert. Il est éventuellement possible d'utiliser un transducteur comme fonction de hachage, mais le calcul des adresses ne sera plus effectué en un temps constant (voir la partie 5).
La probabilité de ce bruit doit rester inférieure à une borne préalablement fixée. On trouvera dans [Bl 72] une méthode utilisant une fonction de hachage qui réduit l'espace nécessaire en autorisant un faible bruit.
La méthode de Robert NIX [Ni-81], décrite ci-dessous, est bien adaptée à la représentation d'ensembles d'exceptions petits par rapport à l'ensemble des mots. Cette méthode, dite du codage surimposé, est une méthode statistique à base de fonctions de hachage. Uniquement valable pour les lexiques, elle offre un compromis espace/vitesse remarquable dans certaines applications.
Definition :
Nous dirons qu'il se produit du bruit lorsque la fonction Membre(X,w) répond que w [[propersubset]] X alors que w [[reflexsubset]] X .
Ces hypothèses sont vérifiées pour de bonnes règles sur les mots :
R est une bonne règle quand pour Y l'ensemble des mots et X l'ensemble des exceptions, on a : |X|<<|Y|.
Une table de bits[2] est utilisée pour stocker le lexique. Initialement tous les bits de la table sont positionnés à zéro, puis on applique à chaque mot w la fonction d'adjonction d'un mot à la table : Ajouter(table,w) . La fonction Ajouter(table,w) calcule k fonctions de hachage hi, définies de l'ensemble des mots possibles dans l'intervalle d'indice de la table. Ces k fonctions fournissent k adresses hi (w), que la fonction Ajouter positionne à 1.
Pour réaliser la fonction Membre(X,w) les k fonctions sont calculées sur le mot w.
De deux choses l'une :
- soit une des adresses hi (w) est positionnée à zéro
alors le mot w n'est pas dans X (en effet Ajouter(table,w) aurait positionné tous les bits hi (w) à 1).
- soit tous les bits des adresses hi (w) sont positionnés à 1
alors w est dans X, sauf si par hasard les adresses générées sont toutes positionnées à 1 bien que le mot w n'ait pas été entré, ce qui correspond au bruit.
La probabilité d'occurrence du bruit se calcule de la façon suivante : pour un lexique X de n mots, k fonctions de hachage et une table de t.n.k bits, la proportion d'erreur à laquelle on peut s'attendre est de (1/t)k. Les paramètres k et t sont choisis en fonction de la place disponible et du taux de bruit voulu. Plus la table et le nombre de fonctions de hachage sont grands plus le bruit est faible.
Exemple :
1) Sur un dictionnaire de 6Mo avec 530.000 entrées :
pour k=10, t=2 la taille de la table est de 1,3 Mo et la probabilité d'erreur est 0,1 % ;
pour k=10, t=8 la taille de la table est de 5,3 Mo et la probabilité d'erreur est de 10-7%.
Mais alors la compression n'est pas intéressante.
2) On trouvera en annexe un exemple d'utilisation sur la règle lexicale : [les mots finissant par -ait sont des verbes, sauf [une liste de 25 mots dont abstrait] ]. Cette règle s'applique à peu de mots. Mais utilisée avec une règle comme : [les mots ayant une terminaison -t sont des verbes sauf une liste de 7762 mots ] la méthode est intéressante. On trouve dans le DELAF 105.530 mots en terminaison -t, 92% de ceux-ci sont des verbes ; la liste des exceptions est trop grande pour être parcourue à chaque application de la règle. Une table de codage surimposé ayant un taux d'erreur de 0,19% occupe 25Ko de mémoire, et nous permet dans plus de 90% des cas d'éviter de parcourir cette liste d'exceptions.
Le codage surimposé s'applique donc bien à des règles lexicales du type :
[si w a pour suffixe le mot u et w n'est pas dans la liste (liste des exceptions) alors w est un (partie du discours donnée)]
On trouvera des exemples de ce type de règles dans [Gu 90].
En pratique pour un taux d'erreur acceptable, notre rapport de compression R peut aller jusqu'à 0,1 (compression au dixième).
Nous avons utilisé, pour parler de la complexité de ces méthodes, la notion de complexité asymptotique, notée O(). Celle-ci nous donne le comportement asymptotique des méthodes étudiées. Des constantes qui n'apparaissent pas dans ces complexités jouent souvent de façon importante sur l'efficacité pratique des algorithmes , comme par exemple, l'influence du nombre des accès disques.
Un point important est le temps de calcul nécessaire pour comparer deux éléments d'un ensemble. Le test de comparaison est utilisé par la plupart des méthodes précédentes. Deux sortes de tests sont employés :
- un test de comparaison de mots, utilisé par les listes et les arbres autres que les ALG.
- un test de comparaison de caractères, utilisé par les ALG.
Notons que la comparaison de deux mots a une complexité de O(l), l étant la longueur du préfixe commun des deux mots alors que le test de comparaison de caractères est constant. Les complexités des deux tests ne sont pas du même ordre.
Nous résumons ici les complexités des différentes méthodes : la complexité de la fonction Membre puis les tailles correspondantes (en mémoire / sur disque) pour le DELAF avec les codes numériques comme donnée associée:
l est une constante qui mesure la longueur moyenne des mots ;
d est une constante qui mesure le temps nécessaire pour un accès disque ;
h est une constante qui mesure le temps de calcul de la fonction de hachage.
les tailles sont pour le DELAF avec les codes numériques
- Listes : O((l+d) log2(n)) -/ 8Mo.
- Arbres AVL, Arbres 2-3 : O( l log2(n)+ d ) 12/8 Mo.
- Arbres ALG : O(l + d) 16/8 Mo.
- Hachage[3] : O(d+h) 2/8 Mo.
Tous ces méthodes neccesitent pour leur mise en oeuvre un espace considérable toujours supérieur ou égal à la taille du dictionnaire sous forme de texte.
Cette représentation a d'autres attraits : de nombreux traitements sont accélérés, notamment les traitements effectués sur l'ensemble des mots. Il est plus rapide de charger l'automate puis de générer le lexique que de lire le même lexique sur disque dur! De plus cette représentation permet la mise au point d'algorithmes de recherche du voisinage d'un mot très rapides. On trouvera en annexe quelques programmes qui montrent l'efficacité de cette représentation pour l'extraction de sous-ensembles du DELAF: Par exemple des programmes qui déterminent les mots contenant une sous-chaîne donnée, les anagrammes d'un mot, les mots s'écrivant sur un ensemble de lettres. La liste n'est pas exhaustive.
Après quelques notations et définitions, nous présentons quelques mises en oeuvre des automates, puis deux algorithmes utilisés pour transformer une liste de mots en automates. Nous exposons à la fin de cette section deux adaptations de la structure d'automate au problème des dictionnaires comportant des codes. Le problème étant défini par les deux questions suivantes :
1) soit w un mot, c un code et X un ensemble de couples (mot,code) :
w est-il un mot du sous ensemble de X des mots associés au code c ?
2) soit w un mot et X un ensemble de couples (mot,code) :
si w est un mot de X, quel est le code c associé a w ?
Pour un ensemble de codes réduit, nous pouvons utiliser des automates en gardant la même vitesse d'accès et un bon taux de compression, ce taux dépend du nombre et de la répartition des codes, le cas des codes grammaticaux étant bien adapté : le code et le suffixe d'un mot sont fortement corrélés.
- un alphabet fini B;
- un ensemble fini d'états noté Q ;
-
une partie I de Q d'états initiaux ;
- une partie T de Q
d'états terminaux ;
- un ensemble fini F de triplets
(p,a,q), où p et q sont des
états et a un symbole de l'alphabet B ; ces triplets sont les
transitions de l'automate.
Figure 9. Un automate déterministe acyclique.
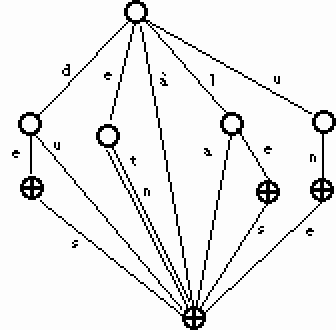
Les automates déterministes sont des automates dans lesquels pour tout état p de Q et pour tout symbole a de B, il existe au plus une transition partant de l'état p étiquetée par a. On demande en plus que I soit réduit à un unique élément, c'est-à-dire que l'automate ne possède qu'un seul état initial.
A moins d'indications contraires, nous considérons dans la suite du texte des automates déterministes. Nous verrons également des automates à plusieurs états initiaux et leurs comportements et utilisations spécifiques.
On notera |Q| le nombre d'états, |F| le nombre de transitions, |B| le cardinal de l'alphabet.
Exemple :
Le langage reconnu par l'automate de la Figure 9. est :
L(A)=
{à,de,des,du,en,et,la,le,les,un,une}.
Cette méthode est efficace pour la fonction Membre(X,e) : on reconnaît un mot en un nombre d'étapes égal à la longueur de ce mot, quel que soit le nombre de mots du langage reconnu, c'est à dire quel que soit le nombre d'entrées du lexique. Les mots sont considérés comme non reconnus dès que le plus long préfixe commun avec le langage reconnu est dépassé.
Nous appelons langage associé à un état s le langage reconnu en prenant s pour état initial (voir la Figure 40. Partie 6), seuls les successeurs de s sont considérés (si (p,a,q) est une transition alors q est un successeur de p).
On parle d'automates acycliques quand il n'existe pas de suite de transitions dans l'automate qui permette de passer deux fois par le même état.
Les automates acycliques sont plus spécialement adaptés au problème des lexiques. Ils ont en effet la particularité de reconnaître des ensembles finis, et réciproquement tout ensemble fini est reconnu par un automate acyclique. De plus nous allons voir qu'on peut profiter de certaines de leurs propriétés pour rendre leur utilisation plus facile et plus rapide que celle des automates généraux.
Des algorithmes de minimisation transforment un automate donné en l'automate minimal qui reconnaît le même langage. La représentation par l'automate minimal peut être extrêmement efficace comme méthode de compression. Un même langage peut être reconnu par des automates dont la taille varie entre n (la taille de l'automate minimal ) et |B|n .
La propriété de minimalité d'un automate est indépendante de la capacité de l'automate à représenter un langage donné. Les expériences sur plusieurs lexiques ont montré l'importance de la minimisation comme fonction de compression. L'ALG représentant le DELAF comporte plus de 2 millions de noeuds. Avec l'automate où seuls les états terminaux sans successeur sont fusionnés, nous obtenons un million d'états. L'algorithme de pseudo-minimisation limite encore le nombre d'états à 400.000. Enfin la minimisation permet d'obtenir un automate minimal comportant moins de 50.000 états, rappellons que le DELAF contient 600.000 mots.
Différentes mises en oeuvre des automates permettent des compromis entre la taille de l'automate et la vitesse de la fonction Transition. Nous allons regarder trois complexités : l'espace utilisé pour représenter l'automate en mémoire, la complexité de la fonction Transition et la complexité de l'algorithme de Transformation qui permet de passer de la mise en oeuvre par listes aux autres mises en oeuvre. Ces trois complexités nous permettent d'estimer les valeurs suivantes :
- vitesse d'accès aux mots du lexique ou du dictionnaire
- encombrement mémoire
- vitesse de la mise à jour de l'automate
La méthode la plus souple est la mise en oeuvre par liste, c'est celle que nous utilisons pour l'ensemble des exemples et la description des algorithmes, étant entendu que l'on peut transformer cette représentation dans toutes les autres.
Posons pour l'instant que la fonction Transition est calculée en un temps t. La fonction Membre(A,w) a donc une complexité de O(t.|p(w)|) où p(w) est le plus long préfixe de w qui soit préfixe d'un mot de L(A).
Remarque : quelquesoit w [[propersubset]] [[Beta]]* max(|p(w)|)=max{|w|, w [[propersubset]] L(A) }. Nous utiliserons dans la suite |w| au lieu de |p(w)|, en effet le choix de la mise en oeuvre n'a pas d'influence sur la profondeur atteinte dans A par la fonction Membre(A,w), de plus si les mots appartiennent au langage reconnu on a |p(w)|=|w|.
Figure 10.
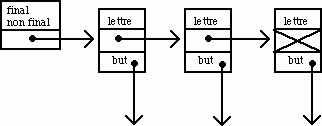
La représentation par listes utilise O(|Q|+|F|) en espace. La complexité de la fonction Transition est, dans le pire des cas: O(|B|) ; soit pour la fonction Membre(A,w): O(|w|.|B|). Il n'y a pas ici de fonction de Transformation. Cette représentation est adéquate pour le DELAF les états ayant en moyenne 2.6 transitions.
Exemple :
Notre alphabet est de quatre lettres, B={a,b,ç}, indicées par 0,1,2,3.
Figure 11.
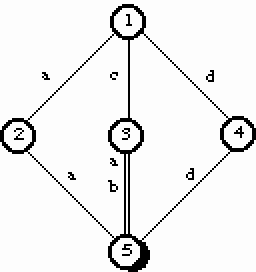
Figure 12.
état\lettre a b c d
1 2 0 3 4
2 5 0 0 0
3 5 5 0 0
4 0 0 0 5
5 0 0 0 0
Remarque
: un deuxième tableau est nécessaire (ou une liste) pour les
états terminaux ; toutes les cases contenant 0 sont
vides et inutiles.On obtient une complexité de O(|B|.|Q|) en espace et un accès direct pour la fonction Transition. La fonction Membre a une complexité de O(|w|). La Transformation est en O(|F|). Notons qu'il faut O(|B|.|Q|) opérations pour initialiser le tableau.
Cette méthode est adaptée aux automates complets où |F|=|B|.|Q|. Le tableau est alors entièrement rempli.
Figure 13.
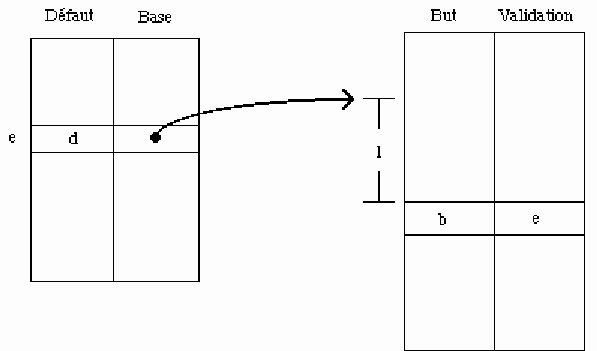
La fonction Transition(e,l) s'écrit alors :
fonction Transition(e,l)
début
si
Validation[Base[e]+l]=e alors
retourner(But[Base[e]+l]
);
sinon/* la condition d'échec est dans le cas où
défaut[e]=e non testé ici */
retourner(transition(Défaut[e],l);
fin;
Base[e] permet de trouver la position des transitions de l'état e dans le tableau But ;
Base[e]+l est la position de la transition par l de l'état e ;
le tableau Validation confirme que l'on a bien une transition de l'état e ;
dans le cas contraire, le tableau Défaut contient le numéro d'un état de suppléance.
Nous avons donc en espace O(|Q|+|F|+|B|). La fonction Transition a une complexité O(p), où p est le nombre de suppléances maximum. La fonction Membre a une complexité O(|w|). Cette représentation se heurte à un problème important : il n'existe pas d'algorithme rapide pour agencer le tableau But de façon idéale. En pratique on utilise un algorithme "glouton" qui place les états sur la première position possible (first-fit), et donne de bons résultats pour des automates peu denses.
Exemple :
Nous utilisons le même automate que dans l'exemple précédent sur les listes.
Nous utilisons les indices suivants pour chaque lettre : a=0,b=1,c=2 etc.
Pour obtenir un tableau bien rempli , nous cherchons à utiliser les trous laissés dans la listes des transitions d'un état, pour y placer les transitions d'un autre état. Ici l'état 2 est placé dans la case (1,b) de la figure. 12, qui est vide ; et l'état 4 dans la cases (2,c). D'où le tableau suivant plus petit , où un état est matérialisé par une position dans le tableau.
Le tableau T[] est indicé par des entiers de 1 à |F|.
Chaque case contient une lettre (le) et un indice de T[] qui indique ou est matérialisé l'état but.
T :
1 2 3 4 5 6 7 8
a,2 a,8 ç d,4 a,8 b,8 d,8 [[circle
multiply
]],[[cir
clemulti
ply]]
Les
lettres servent à différencier l'état auquel la transition
appartient.Nos états ont changé de numéros : 1->1, 2->2, 4->4, 3->5, 5->8.
La fonction Transition(e,l) s'écrit :
fonction Transition(e,l)
début
si T[e+l].le
=l alors
retour(T[e+l].but );
sinon
retour(ECHEC);
fin;
Ce tableau s'utilise de la façon suivante : à une nouvelle lettre du mot, on regarde la case indicée par le numéro de l'état courant additionné de l'indice de la lettre. Si la case ainsi définie contient une transition par la lettre courante, alors la transition existe et nous pouvons l'emprunter. Sinon la transition n'existe pas.
Exemple suite :
Nous utilisons le tableau précédent T[]. L'état initial est en position 1.
Pour le mot ad :
on a T[1+a].le=a et T[1+a].but=2 ; il existe donc une transition (1,a,2) ;
par contre, T[2+d].le=a
il n'existe donc pas de transition d'étiquette d partant de l'état 2, ce qui peut être vérifié sur la Figure 15.
Le mot ad n'appartient donc pas au langage reconnu.
Pour le mot cb :
T[1+c].le=c et T[1+c].but=5 ;
on avance sur l'état 5 ;
T[5+b].le=b et T[5+b].but=8 ;
on avance sur l'état 8 ;
la fin du mot est atteinte, il faut vérifier que l'état 8 est un état terminal dans un tableau ou une liste annexe ; le mot cb est reconnu par l'automate.
Nous avons donc en espace O(|F|+|B|). La fonction Transition a une complexité O(1). La fonction Membre est en O(|w|) .
Il n'est malheureusement pas toujours possible de compacter les états dans un tableau de Taille O(|F|+|B|). Par exemple l'automate qui reconnaît le langage {aa,ab,cb,cc}ne permet pas d'obtenir le compactage maximum. En pratique de bons résultats sont obtenus dans le cas d'automates peu denses, ce qui est le cas de nos automates de lexiques de langues naturelles. R.E. Tarjan [TY 79] propose une méthode de compression des tables peu denses qui s'applique bien ici. (On trouvera dans [Li 83] une description de la méthode). Pour le cas particulier de l'automate du DELAF, le nombre d'états comportant une à deux transitions est très grand, ce qui rend assez aisée la fonction Transformation à partir des listes (voir la courbe en annexe).
Un premier algorithme fabrique pour un langage L donné un automate pseudo-minimal qui reconnaît L en un temps proportionnel à la somme des longueurs des mots de L. Cet algorithme procède à une première minimisation, en comprimant certains suffixes communs à plusieurs mots.
Un second algorithme de minimisation des automates acycliques transforme ensuite l'automate pseudo-minimal en l'automate minimal.
Nous exposons d'abord la fabrication d'un ALG à partir d'une liste, puis notre algorithme de pseudo-minimisation proprement dit. Cet algorithme utilise les suffixes communs des mots de notre langage pour réduire le nombre d'états dans l'automate généré. La pseudo-minimisation permet donc de réduire le coût de la minimisation, dont la complexité dépend du nombre d'états et de transitions.
De deux choses l'une :
- soit ce préfixe est le mot m en
entier, auquel cas l'état atteint par ce préfixe est
transformé en état terminal ;
- soit le plus long
préfixe commun est plus court que m, auquel cas on crée
les transitions nécessaires.
On commence par un arbre réduit à un seul noeud, puis on effectue :
Ajouter(A,"aa") et Ajouter(A,"bb")
Figure 14.
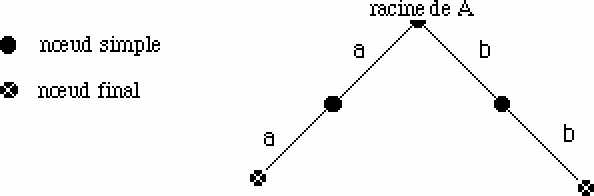
puis Ajouter(A,"b")
Figure 15.
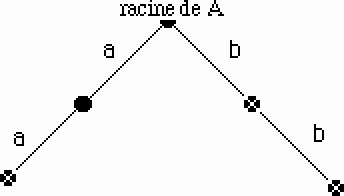
puis Ajouter(A,"ba").
Figure 16.
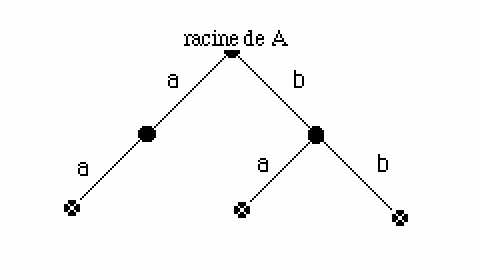
Cette méthode, très simple à mettre en oeuvre, a l'inconvénient de créer un arbre de trop grande taille pour nos dictionnaires. La taille atteinte est celle d'un ALG. De plus la complexité du second algorithme de minimisation est dépendante de cette taille. Nous proposons donc l'algorithme de pseudo-minimisation suivant.
L'algorithme de pseudo-minimisation utilise la notion de plus long suffixe commun entre un mot et un ensemble de mots. Ce plus long suffixe commun nous est utile pour ne pas créer deux fois un chemin commun à deux mots.
Le plus long suffixe commun d'un mot et d'un ensemble est le plus long suffixe du mot qui est aussi suffixe d'un mot de l'ensemble. Il est noté lsc(e,X).
Pour simplifier la recherche du plus long suffixe commun, nous ajoutons les mots à l'automate dans l'ordre lexicographique inverse (les comparaisons lettre à lettre se faisant de droite à gauche), ce qui permet d'entrer consécutivement des mots dont le suffixe commun est le plus long suffixe commun du dernier mot avec l'ensemble des mots déjà entrés. Nous utilisons une variable elsc qui contient le chemin utilisé par le suffixe commun dans le mot précédent.
Le lsc(,) va donc nous permettre de réutiliser le chemin déjà créé dans l'automate.
Regardons sur un exemple le déroulement de la nouvelle fonction Ajouter.
A l'automate initial L(A)=Ø :
Figure 17.
Ajoutons le mot "aaa".
On pose : elsc("aaa",L(A))= T ;
Ici elsc n'est pas défini, on le pose donc égal à l'état T afin d'utiliser l'état T comme seul état terminal sans successeur.
Il n'y a pas de préfixe dans L(A). On crée entièrement le chemin étiqueté par "aaa".
Figure 18.
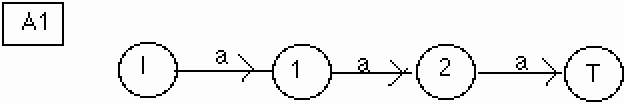
Ajoutons le mot "baa".
On obtient : elsc("baa",L(A))= 1,2,T ; le suffixe commun "aa" de "aaa" et "baa" utilise les états 1,2 et T.
Dés qu'on commence à ajouter "baa", on atteint immédiatement le lsc. Les états du elsc sont donc utilisés :
Figure 19.
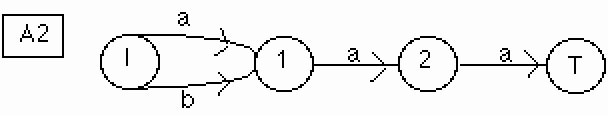
Le chemin 1, 2, T a été utilisé.
Ajoutons le mot "aab".
On a : elsc("aab",L(A))= T.
On suit la transition (I,a,1). L'état 1 a deux prédécesseurs. On ne peut l'utiliser car cela rajouterait le mot "bab" au langage reconnu, il faut donc le dupliquer. L'état 2 doit être dupliqué pour la même raison :
Figure 20.
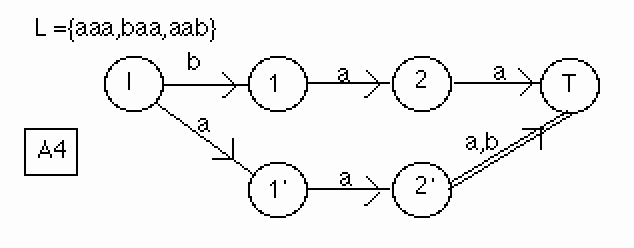
Ajoutons le mot "cab".
On a : elsc("cab",L(A))= 1',2',T.
Un autre problème apparaît ici : l'état 2' a deux transitions sortantes. L'utilisation de cet état entraineraît la création du mot "caa" ; le elsc est donc réduit à T. On obtient l'automate :
Figure 21.
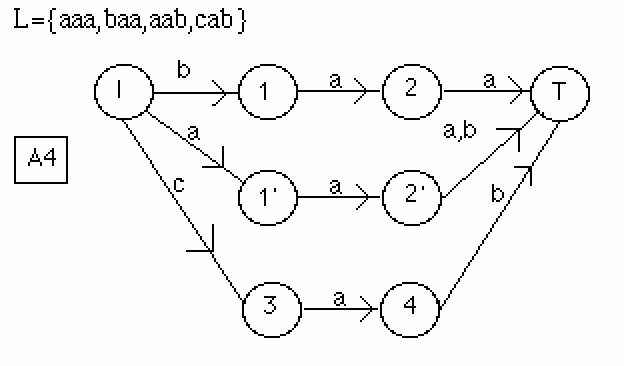
Précisons enfin qu'il ne faut pas utiliser le suffixe commun si celui-ci a été utilisé par le préfixe, comme le montre l'exemple suivant :
Ajoutons le mot "dcc".
Figure 22.
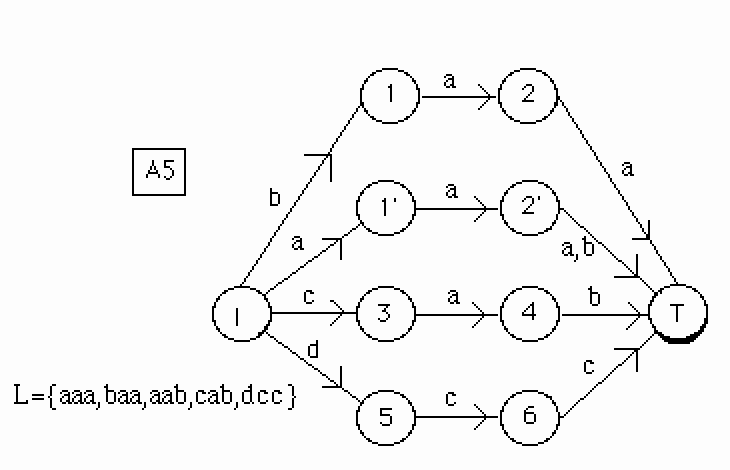
Ajoutons le mot "dccc".
On a : elsc(L(A5)) = 5, 6, T. Or les états 5,6,T ont tous été utilisés par le préfixe "dcc" de "dccc". On ne peut pas se raccrocher au suffixe commun car ceci créerait un cycle..
Figure 23.

Pour gérer ce problème nous marquons de façon temporaire les états utilisés par le préfixe, les états de elcp ne sont utilisés que si ils ne sont pas marqués.
En résumé : l'algorithme de pseudo-minimisation applique la fonction Ajouter à chaque mot dans l'ordre lexicographique inverse. Cette fonction a le comportement suivant :
cas 1 : Tant que (une transition étiquetée par la lettre courante existe et que l'état atteint par cette transition n'a qu'un prédécesseur) alors on avance sur cet état et sur la lettre suivante ;
cas 2 : Tant que (la transition existe mais l'état atteint a plus d'un prédécesseur) on duplique l'état atteint par la transition que l'on redirige vers ce dupliqué. On avance sur le dupliqué et sur la lettre suivante.
cas 3 : Tant que (le lsc n'est pas atteint) on crée une nouvelle transition étiquetée par la lettre courante et un nouvel état sur lequel on avance ainsi que sur la lettre suivante.
Le lsc est atteint:
cas 4 : Tant que (le lsc est marqué) on crée une nouvelle transition étiquetée par la lettre courante et un nouvel état sur lequel on avance ainsi que sur la lettre suivante.
cas 5 : Si le lsc n'est pas marqué, on crée une transition qui y mène et on le suit jusqu'à la fin du mot.
Quand la fin de mot est atteinte dans une des boucles précédentes, soit d le dernier état atteint :
Si d n'est pas terminal, de deux choses l'une :
- Si d a plus d'un prédécesseur, on duplique d en d', et d' devient terminal ;
- Si d a un seul prédécesseur, il devient terminal.
Cet algorithme a une complexité en O(T) linéaire en la taille du lexique.
Cet algorithme utilise le tri lexicographique sur des étiquetages des états en remontant dans l'automate. La complexité est de O(t+n), où t est le nombre de transitions et n le nombre d'états de l'automate.
La minimisation d'un automate consiste à éliminer les états redondants, ayant le même langage associé. Dans le cas général des automates avec cycles, l'algorithme a une complexité de O(nlog(n)), où n est le nombre d'états de l'automate que l'on minimise. Dans le cas des automates acycliques nous avons un algorithme plus rapide.
On utilise une notion de hauteur H définie sur les états :
H(s) =MAX(|w|) ; s.w appartient à T
en d'autres termes, H est égale à la longueur du plus long chemin partant de l'état s, et aboutisant à un état terminal.
Cette hauteur nous permet de partitionner l'ensemble des états Q en une partition notée [[Pi]]. [[Pi]]i représente l'ensemble des états de hauteur i.
On dira que [[Pi]]i est distingué si toute paire d'états de [[Pi]]i est une paire d'états distingués, c'est à dire si les langages associés aux deux états sont différents.
L'intérêt de cette partition est la propriété de hauteur, qui rend le test de l'équivalence de deux états extrêmement simple et rapide.
Propriété de hauteur.
Si pour tout j<i on a [[Pi]]j distingué alors q et q' appartenant à [[Pi]]i sont équivalents si et seulement si pour tout a de B on a q.a = q'.a.
Ceci est plus facile à tester que l'égalité des langages associés.
Il ne nous reste plus qu'à écrire l'algorithme :
Minimisation:
calculer [[Pi]]
fusionner les états de
[[Pi]]0
pour i:= 0 à H(q0)
faire
début
Trier les états de [[Pi]]i par
leurs transitions
fusionner les états
équivalents.
fin.
que l'on peut réécrire comme suit : pour tous les éléments de la partition par hauteur croissante, trier les états par leurs transitions ; et s'ils sont égauxc'est-à-dire équivalents, les fusionner.
Cet algorithme élimine les états équivalents et donc minimise l'automate.
La complexité de l'algorithme dépend de la complexité du tri. Nous utilisons un tri inspiré du tri lexicographique qui est linéaire, d'où la complexité O(|Q|+|F|). Cet algorithme est décrit en détail dans la section 6. Le calcul de [[Pi]] demande de parcourir l'automate et nécessite une mémoire additionnelle d'un entier par état, soit O(|Q|) en espace et O(|F|) en temps.
La boucle trie l'ensemble des états par morceaux disjoints. On a donc pour le tri une complexité en [[Sigma]]O(f(|Qi|), où O(f(n)) est la complexité de la fonction de tri et Qi les états de hauteur i. Nous proposons dans la section 6 un tri inspiré du tri lexicographique, qui permet de trier nq états ayant un total de nt transitions en O(nq+nt) étapes.
Nous marquons les états affectés par l'insertion (ou la suppression). Ce marquage permet, au moment de la minimisation, de ne comparer que les états susceptibles d'être fusionnés.
La fonction Insérer utilise uniquement les cas 2 et 3 de la fonction Ajouter.
Tant que le chemin existe on duplique les états de ce chemin ;
puis on crée des états pour finir le mot.
Le mot est bien ajouté au langage reconnu, et un ajout involontaire d'un autre mot est évité.
Remarque : il est possible de grouper plusieurs insertions et/ou suppressions et d'effectuer ensuite une seule minimisation.
Ce fort taux de compression permet de mettre dans la mémoire vive de l'ordinateur le dictionnaire entier. La fonction Membre est ainsi considérablement accélérée car il n'est plus nécessaire de faire appel aux mémoires de masse, toujours très lentes (l'accélération peut être d'un facteur 103). Il est plus rapide de charger l'automate en mémoire et de générer la liste de mots que de lire cette liste sur disque.
Cette répresentation facilite l'écriture des programmes de recherche de motifs, recherche de voisins d'un mots, des anagrames etc .
Les notions de voisinage d'un mot et de distance entre mots sont utilisées par les correcteurs orthographiques et par les logiciels d'analyse pour les systèmes de lecture optiques de textes (O.C.R.) La rerprésentation par automate accélère ces fonctions.
Nous définissons la distance entre deux mots m1 et m2 comme le coût de la suite d'opérations élémentaires la moins coûteuse qui permet de transformer m1 en m2. Les opérations élémentaires sont les suivantes :
effacement : écrit --> écrt coût = 1
insertion : écrit --> écriot coût = 1
substitution : écrit --> écrot coût = 1
permutation : écrit --> cérit coût = 1
substitution simple : écrit -->ecrit coût = 0.5 (toutes les substitutions par accent ).
L'ensemble des mots à une distance donnée croît considérablement vite. Dans une représentation par automates, la combinatoire est limitée aux préfixes des mots à distance donnée, et donc fortement réduite. Une autre possibilité, qui n'en est qu'au stade de projet, est d'utiliser grâce à un automate la notion de plus grande sous-suite commune, notion plus adéquate pour les correcteurs orthographiques. D'autres utilisations de l'automate sont présentées en annexe : anagrammes, carrés magiques.
La représentation par automates permet d'écrire des algorithmes de recherche de motifs qui sont plus rapides que leurs homologues appliqués à la liste de mots.
Ainsi une fonction de recherche d'expressions rationnelles sur le dictionnaire sous forme d'automate est en moyenne beaucoup plus rapide que sur la liste de mots en particulier pour les expressions contenant le caractère de début de mot.
pomme de terre
demande que l'analyseur reconnaisse d'une part le mot composé, et d'autre part les trois mots simples. Les transitions par un séparateur demandent une gestion spécifique, qui peut être un autre appel simultané de la fonction Membre. Ceci ne pose pas de problème sur les automates.
Cette représentation permet d'éliminer de la liste des mots simples des mots comme :
hui, aujourd, parce, priori
et ainsi de lever certaines ambiguïtés facilement, la séquence de mots libres n'existant pas.
Les automates déterministes acycliques multi-terminaux sont des automates où l'on a défini plusieurs ensembles T d'état terminaux.
Notre automate A devient:
(Q,B,I,F,T1,T2,...,Tn)
Ti est un sous-ensemble de Q. Un état peut appartenir à un unique ensemble d'états terminaux ou à plusieurs, en fonction des besoins. Nous considérons dans les exemples suivants qu'un état appartient à un ensemble terminal au plus. Les codes du DELAF sont définis de façon à ce qu'un mot soit associé à un seul code.
Un mot est reconnu de la même façon que par un automate standard ; l'indice de l'ensemble terminal atteint est fourni en lieu et place de l'information d'appartenance simple.
L'automate A représentant le DELAF, où nous avons 8400 codes associés, est de la forme : (Q,B,I,F,T1,...,T8400).
Ce type d'automate permet d'une part d'avoir accès à la notion d'automate minimal, à la différence des transducteurs. Le compactage de l'automate est donc possible ; la taille utilisée reste raisonnable. D'autre part les mêmes fonctions et fonctionnalités que pour les automates acycliques standards sont disponibles. En particulier, les algorithmes de création et de minimisation sont utilisables avec peu de transformations.
L'automate à multi terminaux du DELAF à 76000 états et 177000 transitions, il est possible de le stocker avec 1Mo de mémoire.
Selon le même principe, mais avec une approche inverse, on défini un automate à multi-initiaux (équivalent à un automate standard du point de vue théorique, comme d'ailleurs les multi-terminaux ). Un automate à multi-initiaux A est un uplet :
(Q,B,q1,...,qn,T,F)
où les qi sont n états initiaux distincts.
Dans la figure suivante, nous avons représenté un automate à deux états initiaux, l'un reconnaissant des déterminants, l'autre des conjonctions.
Figure 24.
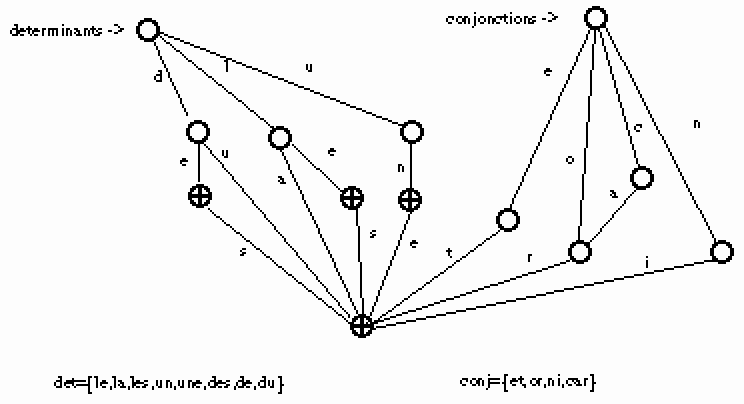
Nous pouvons reprendre les remarques, concernant la taille et les programmes, faites pour les automates à multi-terminaux.
Ces automates peuvent s'intégrer facilement à un système de grammaires, ou à des utilitaires définis sur des constructions syntaxiques utilisant les parties du discours. Dans cette représentation, un mot peut appartenir à plusieurs sous-ensembles, le partitionnement des mots est plus fin.
Le modèle suivant cherche à tirer parti des deux approches afin d'obtenir un dictionnaire comprimé, et avoir accès à des données indexées par les mots. Pour cela on utilise le fait que l'automate acyclique du DELAF est pour une grande part un ALG. Cette méthode présente des avantages par rapport au système de hachage présenté dans la section 4., qui nécessite une table d'adresses supplémentaire de plus de 2Mo. Ici, seulement 90Ko supplémentaires sont néccessaires.
Définitions :
L'ALG interne d'un automate acyclique est l'ensemble des états q qui appartiennent à des chemins partant de l'état initial et composés uniquement d'états de degré entrant 1 (soit un seul prédécesseur direct) .
Dans la figure suivante l' ALG interne ressort en gras.
Figure 25.
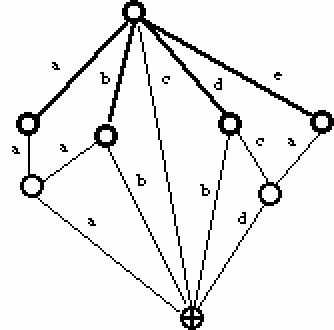
Si l'on prend pour racine de notre ALG l'état initial de l'automate, et pour descendance uniquement les états ayant un seul prédécesseur (ou ascendant) direct et accessibles uniquement par un chemin qui ne passe que par des états ayant cette propriété, nous obtenons un ALG qui partitionne par les préfixes notre ensemble de mots.
Exemple :
Dans l'automate du DELAF le préfixe entro- a cette propriété. On rajoute à cet état un pointeur sur un fichier qui contient la fin des mots commençant par entro-, ainsi que leurs définitions.
-bliger, V3 -pie , -pion -que -uvert -uvrir
Le nombre de pointeurs supplémentaires par rapport à l'automate est égal au nombre de feuilles de L'ALG ainsi défini. La taille des fichiers peut rester grande, mais on y entre à coup sûr. En effet avant de chercher le mot dans la liste, on vérifie grâce à l'automate qu'il existe bien. De plus on ne cherche plus le mot en entier, mais le suffixe qui manque.
L'ALG interne du DELAF permet de séparer les mots en 28000 groupes, dont le plus grand contient 375 entrées. En moyenne ces groupes comportent 20 entrées. Les mots d'un même groupe se succèdent dans le dictionnaire rangé dans l'ordre lexicographique. Il est ainsi possible de garder le dictionnaire sous une forme usuelle et donc agréable.
La mise à jour d'un dictionnaire utilisant cette structure de données devient plus complexe, on peut changer directement la donnée associée à un mot, par contre pour ajouter ou supprimer un mot trois étapes sont nécessaires :
-mettre à jour l'automate O(|w|)
-minimiser l'automate O(|F|)
-recalculer L'ALG interne O(|F|+|Q|).
Cette mise à jour est donc une opération coûteuse par rapport à d'autres systèmes de bases de données où les insertions et suppressions se font plus rapidement, ce nouveau modèle s'applique donc à des bases de données où les mises à jour sont peu fréquentes .
Ces transducteurs de phonémisation ont deux applications très intéressantes : ils peuvent être employés par des correcteurs orthographiques qui utilisent la phonémisation pour proposer le mot correct, comme c'est le cas pour l'annuaire électronique. D'autre part, l'utilisation en reconnaissance de la parole semble prometteur, soit directement le transducteur à retour du DELAP soit un transducteur de stockage des sons.
Nous présentons ci-après quelques généralités sur les transducteurs, les transducteurs à retour et le principe du plongement comme méthode de minimisation des transducteurs.
- Q un ensemble fini d'états
- B1 un alphabet fini de symboles
d'entrée
- B2 un alphabet fini de symboles de sortie
- I un
ensemble d'états initiaux (réduit à 1 seul état en
général)
- T un ensemble d'états dits terminaux.
- F
un ensemble de quadruplets (q, m1, m2, p)
où p et q sont des états. m1 est un mot sur l'alphabet B1 et m2 un mot sur l'alphabet B2, qui définissent les transitions entre états : m1 est le mot lu pour parcourir la transition et m2 le mot émis par l'utilisation de cette transition.
Nous utiliserons ici des transducteurs dits sous-séquentiels où une émission peut être ajoutée aux états terminaux.
Un mot est reconnu par un transducteur de la même façon que par un automate, mais de plus un mot est émis. On notera T(w) le mot émis par le transducteur T quand il reconnaît le mot w.
Malheureusement les transducteurs n'ont pas toutes les propriétés intéressantes des automates, en particulier il n'existe pas de transducteur minimal. Il n'existe pas non plus pour le moment d'heuristique qui donne des résultats satisfaisants pour réduire leur taille, or ceci est fondamental, en effet le transducteur du DELAP non minimisé est trop grand pour nous.
Nous utilisons ici des transducteurs dits sous-séquentiels, où une information est émise par les états terminaux. Cette information est émise uniquement dans le cas où la fin du mot est atteinte. La Figure 27. présente de tels états terminaux.
Nous allons regarder en priorité des transducteurs acycliques qui, comme les automates, reconnaissent des ensembles finis. De nouveau l'acyclicité offre des possibilités algorithmiques qui n'existent pas sur les transducteurs standards.
Pour des transducteurs acycliques où sur les étiquettes de transitions l'entrée est réduite à un seul symbole , nous pouvons utiliser la même notion de minimalité que celle utilisée pour les automates. Pour les transducteurs l'alphabet d'entrée étant variable la notion de minimalité n'existe plus, cf figure 26.
Nous définissons ici l'équivalence de transducteurs. Cette équivalence permet de définir la minimisation des transducteurs.
Deux transducteurs T1 et T2 définis sur les mêmes alphabets sont équivalents si et seulement si les deux affirmations suivantes sont vérifiées :
1) L(T1) = L(T2) = L
2) [[universal]] [[omega]] [[propersubset]] L,
T1([[omega]]) = T2([[omega]])
autrement dit : si les langages reconnus sont identiques, et si pour les mots de ce langage l'émission est identique pour les deux transducteurs.
Il n'existe pas d'algorithme qui nous permette de rester dans l'ensemble des transducteurs équivalents et nous assure une réduction soit du nombre d'états, soit du nombre de transitions.
Le plongement permet une autre forme de minimisation. Nous ne voulons plus garder ici que la fonction d'émission,et non plus le langage :
T1 est plongé dans T2 si et seulement si les deux affirmations suivantes sont vérifiées :
1) L(T1) Ì L(T2)
2) [[universal]] [[omega]] [[propersubset]] L(T1)
T1([[omega]]) = T2([[omega]])
Regardons par exemple le DELAP qui est un transducteur :
Figure 26.
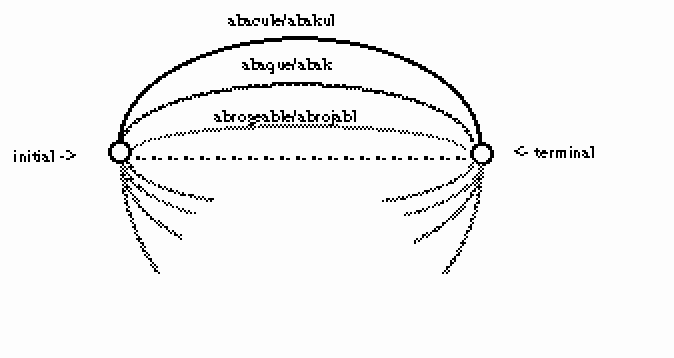
Cette version T1 -- le DELAP sous forme de listes -- du transducteur ne nous apporte rien sur le plan algorithmique. Le temps de calcul nécessaire au choix d'une transition à emprunter est celui d'un algorithme sur les listes.
La version T2 suivante utilise les propriétés d'accès des automates. L'espace utilisé reste très grand. Le transducteur T2 se construit comme un automate déterministe limité à l'alphabet d'entrée. Nous ne pouvons plus utiliser le principe du plus long suffixe commun du fait des émissions. Quand on effectue cette construction, qui est plutôt celle d'un ALG, il faut repousser les émissions tant qu'elles sont ambiguës. Dans la liste de couples (mot, émission) suivante, il est nécessaire d'avoir lu le mot en entier, ou au moins 4 lettres, pour avoir une émission non ambiguë. La Figure 27.présente une liste de mots et le transducteur qui la représente :
Figure 27.

Après lecture d'une seule lettre, l'émission est ambiguë : ce peut être un a, comme dans le mot ail, ou un è comme dans aile, d'où l'existence de la transition a/[[epsilon]] (le [[epsilon]] note une absence d'émission). L'émission n'est pas ambiguë dans le cas d'un mot d'une seule lettre, ce ne peut alors qu'être un a. L'état terminal qui émet a est noté $/a dans la Figure 27.
Après lecture de deux lettres, l'émission est encore ambiguë, d'où la transition i/[[epsilon]]. De même, quand la troisième lettre, un l, est lue, l'émission reste toujours ambiguë, d'où une transition l/[[epsilon]]. Enfin la quatrième lettre, un e, nous assure une émission non ambiguë, d'où la transition e/èl où èl est émis. La lettre s ne change rien à la prononciation précédemment émise, d'où la transition s/[[epsilon]].
Nous utilisons ici des transducteurs sous-séquentiels où sur chaque état terminal, une émission est définie au cas où l'état serait utilisé comme état terminal, sur la Figure 27 c'est le cas pour tous les états sauf l'état initial. Ces transitions sont notées $/ .
Le transducteur présenté Figure 27. est équivalent au transducteur de la Figure 26. en ce qu'il permet de représenter les mêmes langages, mais présente de bien meilleures propriétés algorithmiques. En effet la fonction Membre prend maintenant un temps proportionnel à la longueur du mot recherché. Néanmoins sa gourmandise en espace mémoire reste importante. On va donc chercher à "minimiser", au sens des automates, ce transducteur. Pour cela, le transducteur est vu comme un automate sur l'alphabet B3, défini par les couples de B1XB2* .
Cette minimisation n'a malheureusement pas beaucoup d'effet sur notre transducteur. La taille du nouvel alphabet étant très importante, peu d'états sont équivalents ; d'où une minimisation de moindre importance. De plus, les émissions étant rejetées en fin de mots, les transitions en fin de mots se trouvent être les plus chargées en émission.
Ce type de transducteur n'est envisageable que dans le cas où l'on dispose d'une donnée de petite taille (par rapport à la machine utilisée).
Pour améliorer l'efficacité de la minimisation, nous devons réduire la taille de l'alphabet B3 et pour cela éviter de trop repousser les émissions en fin de mot. Dans ce but nous introduisons un nouveau type de transducteur.
Définition :
Le Transducteur à Retour : TR = ( Q, B1, B2, I, T, F)
Seule la définition des transitions est changée.
F est un
ensemble de quintuplets (q, m1, m2, n, p) où q et p sont des
états, m1 une lettre de B1, m2 un mot de B2 et n un entier positif ou
nul.
Une étiquette de transition est donc un triplet E/S/R (entrée / émission / retour), où le retour est une valeur entière positive ou nulle, qui permet de revenir sur les émissions précédentes.
Pour notre exemple précédent avec {a,ai,ail,...ailes} le transducteur obtenu est :
Figure 28.
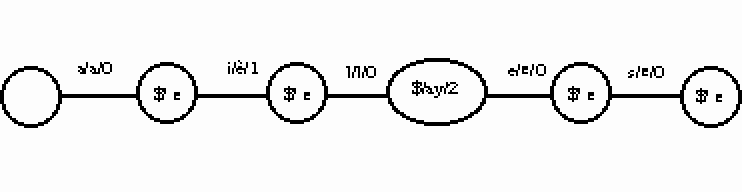
Pour choisir quelle lettre est émise sur une transition, on emploie une approche markovienne utilisant les fréquences des différentes émissions. Ainsi, pour reprendre notre exemple : 99.9% des mots du DELAF commençant par a ont une émission qui débute par a. Pour le premier a, il n'y a pas de retour possible car aucune émission n'a encore eu lieu. La transition est a/a/0. Puis 88% des mots commençant par ai ont pour émission commune le phonème è, d'où la transition i/è/1 qui doit être interprétée comme un retour d'une lettre en arrière sur l'émission du a précédente ; suivi de l'émission d'un è.
Sur cet exemple, remarquons que toutes les transitions sont conformes à la règle "naturelle" : un a donne un a , un l donne un l. Remarquons surtout les deux dernières lettres muettes : ces transitions de lettres muettes en fin de mot sont justement ce qui permet une minimisation intéressante. Les transitions "naturelles" vont être moins nombreuses, donc l'alphabet B3 sera plus petit, d'où une minimisation plus efficace.
Seuls les mots exceptionnels comme aeschne vont générer des transitions étranges par rapport à la règle empirique de phonémisation.
Ce type de transducteurs "fait sur mesure" pour le DELAP peut fournir un outil théorique pour d'autres transductions.
Munis de ce transducteur TR1 qui se construit aussi facilement que T1, nous pouvons construire un transducteur minimisé TR2 théoriquement beaucoup plus petit, grâce à la forme de TR1. Ceci n'a pas encore été expérimenté sur le DELAP entier mais est en cours de réalisation.
Dans le modèle de transducteur et de construction que nous venons de voir, la minimisation est plus efficace, mais l'existence d'exceptions désorganise les émissions et ne permet pas une minimisation idéale, bien que nous ayons beaucoup mieux réparti les émissions sur l'ensemble des transitions.
Les exceptions méritent une gestion séparée. Cette gestion se fait de la façon suivante : une exception est définie comme un mot contredisant la méthode de fabrication précédente qui repousse en fin de mot les émissions. La valeur de retour est très grande, supérieure ou égale à 3 par exemple. Ces mots sont éliminés du dictionnaire et placés dans un ALG annexe, l'ensemble d'exceptions doit être assez petit. Le transducteur obtenu après minimisation devrait être petit. Si ce n'est toujours pas le cas, nous pouvons alors essayer une dernière méthode qui utilise la propriété de plongement décrite plus haut.
1) un dictionnaire d'exceptions contenant les mots et leur émission ;
2) un automate minimal reconnaissant l'ensemble de mots de notre transducteur ;
3) un transducteur (qui peut contenir des cycles).
Les éléments 1) et 2) sont mis en oeuvre simplement avec un ALG et un automate acyclique.
Le transducteur 3) est le premier transducteur à cycles que nous employons. Sur ce transducteur, nous allons utiliser un système de minimisation qui ne conserve que le plongement : nous conservons uniquement le fait que les émissions sont identiques pour les deux transducteurs si le mot fait partie du langage reconnu par le premier.
Ici nous ne cherchons plus à garder constant l'ensemble des mots reconnus, mais à garder la transduction. La minimisation procède par élimination de sous-transducteurs associés à des états différents de l'état initial. Un état, ainsi que tous ses successeurs, est éliminé si le sous-transducteur associé se plonge dans le reste de la transduction.
Le transducteur défini dans la Figure 29 :
Figure 29.
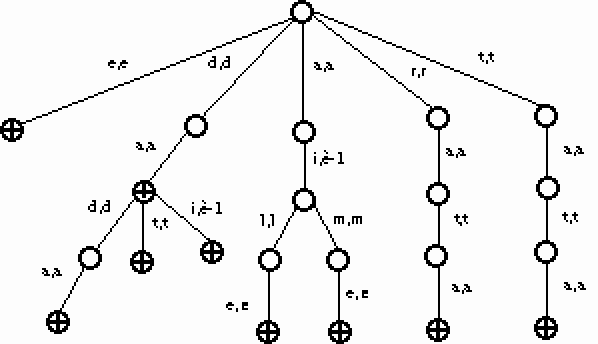
et celui défini dans la Figure 30 :
Figure 31.

émettent les mêmes phonémisations pour les mots reconnus.
Un état
 indique que l'on peut reprendre à l'état initial pour la suite de
la phonémisation.
indique que l'on peut reprendre à l'état initial pour la suite de
la phonémisation.
Pour transformer l'un en l'autre, on commence par parcourir toutes les transitions arrivant sur des feuilles (en effet nous partons d'un arbre) et regarder s'il existe une transition identique partant de l'état initial. C'est le cas pour les transitions a,a et t,t. La transition e,e n'est pas prise en compte car elle est déjà sur l'état initial. Ces transitions sont purement et simplement éliminées. De nouvelles transitions amenant à des feuilles apparaissent. On réitère cette opération tant que toutes les transitions arrivant sur des feuilles ne sont pas différentes de celle de l'état initial. On obtient le transducteur suivant :
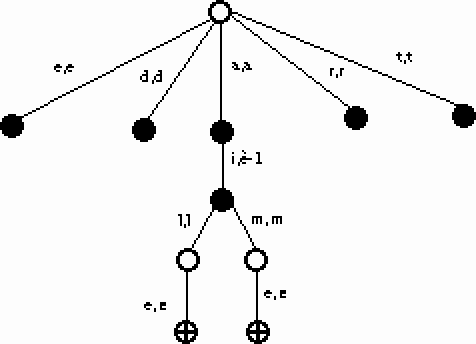
Figure 32.
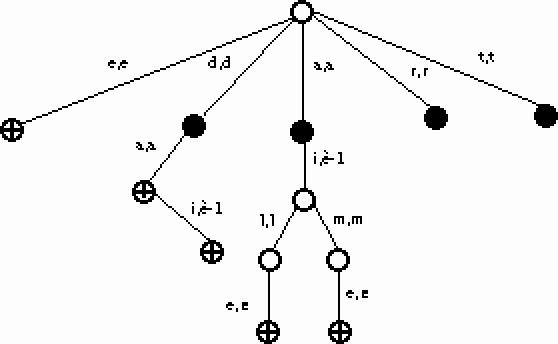
Regardons maintenant les arbres de hauteur 2 : soit ai,è ; le,l et me,m . Un seul de ces trois arbres se retrouve en partant de l'état initial : l'arbre ai,è . On peut donc éliminer cet arbre. On reprend sur les feuilles ainsi crées. Ici uniquement la transition d,d. Elle est sur l'état initial, donc rien n'est changé.
Si on regarde les arbres de hauteur 3, on ne constate aucun changement. Il n'y a pas d'arbre de hauteur 4 distinct de l'état initial, donc l'algorithme se termine.
Cette méthode est heuristique, nous ne pouvons pas savoir si le transducteur obtenu est le plus petit transducteur dans lequel plonge le transducteur initial. Mais un intérêt crucial de ce transducteur est de proposer une émission pour les mots inconnus, qui ne font pas partie du lexique de départ. Le transducteur présenté Figure 28. phonémise correctement tous les mots de la forme ((d+t+r)(a+ai))*, tous les mots faits des syllabes da, dai, ta, tai, ra, rai.
Toutes les méthodes que nous venons de voir sont valables pour des transductions acycliques, où la fonction que nous cherchons à décrire par un transducteur est définie sur des lettres --ce qui est le cas de la phonémisation-- et où l'ensemble des exceptions est réduit.
Dans le cas de la phonémisation, nous avons une fenêtre de 5 lettres, car une émission est toujours possible après la lecture de 5 lettres, qui est réductible, en éliminant les exceptions, à une fenêtre de 3 lettres. On parlera d'une fenêtre de 5 lettres réductible à 3.
Nous avons appliqué de façon automatique les méthodes décrites pour des fonctions qui ont des fenêtres de petite taille (<3). Si notre donnée ne vérifie pas les conditions sur l'alphabet et sur la fenêtre, le transducteur des exceptions sera très gros, ce qui ne fera que reporter plus loin le problème.
- au mot du DELAS dont il est une des flexions ;
- à une table du Lexique-grammaire ;
- à une définition du mot au sens usuel des dictionnaires.
Les automates multi-terminaux sont dans ces cas des ALG, or ceux-ci sont trop gourmands en espace. Le principe de l'ALG interne est délicat à mettre en oeuvre.
Nous nous proposons ici d'utiliser un automate transformé en transducteur de hachage. La transduction fournit une valeur de hachage pour chaque mot. Cette fonction de hachage est adaptée à des supports comme les disques optiques ; on peut utiliser de grands fichiers indexés.
Cet automate est défini avec le même graphe, et les étiquettes des transitions sont réduites à l'alphabet d'entrée. Nous appelons cet automate automate des entrées.
Exemple :
Si (1, a, b, 2) est une transition du transducteur, alors l'automate des entrées a une transition (1, a, 2).
Nous nous intéressons ici à des transducteurs construits à partir d'un automate des entrées acyclique, déterministe et minimal. La transduction est déterministe. Remarquons qu'avec ce principe on ne peut pas obtenir le transducteur du DELAP, des suffixes communs à plusieurs mots ayant des phonémisations différentes.
Nous avons trouvé pour ces transducteurs deux utilisations pratiques d'un grand intérêt. Il est possible de définir avec l'automate du DELAF une fonction de hachage parfaite pour ce dictionnaire, n'entraînant pas de collisions, et permettant un remplissage parfait d'une table de taille minimale. Cette méthode, de plus, se généralise bien. Par ailleurs ce même automate peut être transformé en compresseur de textes écrits en français.
Regardons d'abord comment se calcule le cardinal du langage reconnu par un automate.
Nous avons défini la notion de sous-automate associé à un état s ; c'est l'automate normalisé obtenu en utilisant s comme état initial. Nous allons définir le cardinal d'un état comme la somme des cardinaux de ses successeurs directs, plus 1 si il est terminal.
Définitions :.
Le cardinal d'un état noté Carde est le cardinal du langage du sous-automate qui le reconnaît.
Il se calcule avec la définition récursive suivante :
Carde(s) = somme (Carde(q) tel que (s, a, q) [[propersubset]] F , a [[propersubset]] B , q [[propersubset]] Q) + 1 si s [[propersubset]] T
La fonction récursive s'écrit :
fonction carde(s)
var i:integer;
début
Si s->final alors i:=1 /*si le mot vide est dans L(A(s))*/
sinon i:=0;
pour toutes les transitions t de s
i := i+ carde(t->but);
s->Carde = i;
retour(i);
fin.
Proposition : on a l'égalité
|L(A)| = Carde(q0)
Preuve : la fonction Carde calcule le nombre de chemins terminaux du graphe de A, donc le nombre de mots reconnus.
Définitions :
De même on défini le cardinal noté Cardt d'une transition t partant d'un état s comme la somme des cardinaux des états buts des transitions de s étiquetées par des lettres lexicographiquement inférieures à l'étiquette de t.
Ce qui se calcule de la façon suivante :
Cardt(s, a, s') = somme (Carde(q), tq (s, a', q) [[propersubset]] F avec a'< a )+ 1 si s [[propersubset]] T
où < est l'ordre lexicographique sur B.
fonction cardt(s)
var i:integer;
début
Si s->final alors i:=1 /*si le mot vide est dans L(A(s))*/
sinon i:=0;
pour toutes les transitions t de s dans l'ordre alphabétique des étiquettes
début
t->Cardt := i;
i := i+ carde(t->but);
fin
s->Carde = i;
retour(i);
fin.
C'est la deuxième notion qui va nous être la plus utile pour notre fonction de hachage. En effet nous avons la propriété suivante :
Proposition :
soit w un préfixe d'un mot de L(A)
Si t1,t2,...,t|w| est la suite des transitions que l'on utilise pour reconnaître ce préfixe
alors ISU(i=1;|w|; Cardt(ti)) est le nombre de mots de L(A) lexicographiquement inférieurs à w.
Pour la mise en oeuvre, deux méthodes sont possibles. Nous pouvons calculer Carde pour tous les états de A, et faire le calcul de Cardt au moment de la reconnaissance du mot. Cette première méthode est adéquate dans le cas d'une mise en oeuvre par listes de l'automate, car elle ne demande que O(|Q|) en espace additionnel et ne change pas la complexité O(|B|.|w|) de la fonction Membre. Dans le cas d'une représentation au moyen de tableaux, le parcours de l'ensemble des transitions lexicographiquement inférieures est nécessaire, d'où une perte de vitesse pour la fonction Membre, qui passe de O(|w|) à O(|B|.|w|).
En résumé cette méthode nécessite O(|Q|) de mémoire additionnelle, et la complexité de la fonction Membre devient O(|B|.|w|).
L'autre méthode consiste à placer les valeurs de Cardt(t) sur chaque transition t de A. Elle nécessite une mémoire additionnelle de O(|F|), mais la complexité de la fonction Membre reste inchangée quelle que soit la mise en oeuvre.
Exemple :
Sur le transducteur de la Figure 33., dont le squelette est l'automate de la Figure 4., sont calculées les valeurs de Carde et Cardt pour tous les états et transitions.
Figure 33.
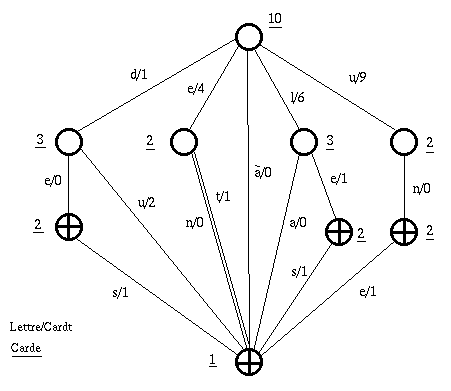
Cette fonction de hachage est construite en deux étapes :
- la fabrication de l'automate minimal en O(T)
- le calcul des Cardt en O(|F|)
La mise à jour de la fonction est faite en trois étapes :
- rajouter (ou supprimer) n mots de longueur totale l : O(l)
- minimiser l'automate : O(|F|)
- recalculer les Cardt : O(|F|)
Dans le cas du DELAF, et en utilisant les Cardt sur les transitions avec une mise en oeuvre par tableaux compactés, l'automate occupe 800k. Il faut ajouter à cette valeur un tableau en O(n), n étant le nombre de mots. Ce tableau donne l'adresse exacte sur disque (cf annexe utilisation avec CD-ROM).
si x1 x2...xn = y1 y2...yp avec xi,yi [[propersubset]] C
alors n = p et xi = yi
On dit d'un ensemble C de mots qu'il est préfixe si et seulement si aucun mot de C n'est préfixe d'un autre mot de C. Tout ensemble préfixe est un code, dit code préfixe.
Le codage de Huffman.
On trouvera dans [Zip-90] une description complète du codage de Huffman [Hu 51], de la méthode de construction de l'arbre et d'un compresseur qui utilise une version adaptative de ce codage.
L'arbre de Huffman utilise la propriété suivante : un code préfixe correspond à la liste des chemins menant de la racine aux feuilles d'un arbre, chaque feuille codant une lettre. Le principe du codage de Huffman est de créer des codes d'une longueur inversement proportionnelle à la fréquence d'apparition des lettres dans un texte. Pour cela on construit un arbre de hauteur pondérée minimum, qui nous fournit un code préfixe de longueur moyenne minimum. Voire Figure 36 page 77 un exemple d'arbre de Huffman.
Définitions :
La hauteur pondérée d'un arbre est la somme :
[[Sigma]] l(a) p(a) pour tout symbole a [[propersubset]] B
où l(a) est la longueur du chemin de la racine à la feuille qui code a.
On dit d'un automate qu'il est à délai d,d>=1;
ssi [[universal]] q [[propersubset]] Q, [[universal]] |w| [[propersubset]] Bd,w=x1,x2,...,xd, si il existe deux chemins
(q,x1,q1)(q1,x2,q2)...(qd-1,xd,qd)
(q,x1,q'1)(q'1,x2,q'2)...(q'd-1,xd,q'd)
alors q1=q'1.
La fonction de compression est notée [[Gamma]] et la fonction de décompression [[Gamma]]-1.
La compression de texte a pour but de réduire le nombre de symboles nécessaires à leur représentation. Dans les applications, la compression de texte est utilisée dans le but d'économiser l'espace de stockage et le temps de transmission. Nous sommes intéressé par des méthodes de compression n'entraînant pas de perte d'information. (Par exemple une compression de textes français consistant à éliminer les accents implique une perte d'informations). Nos fonctions de compression sont donc injectives.
Les algorithmes de compression décrits ici ne sont pas universels (ils ne s'appliquent pas sur des programmes ou des fichiers binaires). Ils sont adaptés à la compression de textes en français, et peuvent s'appliquer avec d'autres dictionnaires à d'autres langues.
La possibilité de comprimer un texte est liée à ce qu'on appelle intuitivement la redondance. Cette redondance peut être lexicale, syntaxique ou sémantique. Elle est liée au fait qu'une suite de caractères constitue un mot correct ou une phrase correcte si elle satisfait à certaines règles.
La règle bien connue de tous que nous cherchons à exploiter est : les textes français sont essentiellement composés de mots français.
La compression de textes a fait l'objet de nombreuses recherches ; il existe deux grandes familles de compresseurs :
- Les algorithmes statistiques, dont le plus célèbre est le codage de Huffman qui utilise un code préfixe de longueur moyenne minimum construit à partir des fréquences d'apparition des lettres à traiter. Nous utilisons cet algorithme dans un de nos compresseurs. Ces algorithmes statistiques utilisent la redondance de caractères : plus un caractère est fréquent, moins il apporte d'information. La commande "pack" d'UNIX met en oeuvre le codage de Huffman.
- Les algorithmes par facteurs fonctionnent en comprimant des facteurs du texte. Un dictionnaire des facteurs du texte déjà codé est utilisé pour coder le reste du texte. La commande "Compress"d'UNIX est une mise en oeuvre de l'algorithme de Ziv et Lempel [76] proposée par Welch [We 84].
La compression de textes en langue naturelle reste un problème ouvert depuis les expériences de Shannon [Sh 51] qui a mesuré de façon expérimentale l'entropie de l'anglais. Hansel, Perrin et Simon [HPS-91] montrent que l'entropie permet de calculer un minorant du taux de compression, qui réciproquement donne un majorant de l'entropie. Les résultats pratiques des commandes "Pack" et "Compress" fournissent un taux de compression avoisinant 0.5 ; alors que l'expérience de Shannon, que nous présentons ci-dessous, prévoit une borne inférieure égale à 0.1.
Expérience de Shannon :
Un sujet ayant lu un nombre fixé de caractères successifs d'un texte doit deviner le caractère suivant. Il est éventuellemnt corrigé si sa prédiction se révèle fausse, et il recommence alors. Dans cette expérience toutes les redondances possibles sont donc prises en compte, le sujet humain utilise toutes ses connaissances et intuitions, formelles et sémantiques, pour faire sa prédiction. L'expérience a été effectuée sur un alphabet de 27 lettres.
Les compresseurs présentés ici vont nous apporter une information très intéressante sur l'entropie lexicale, qui , on peut l'espérer, nous donnera des intuitions sur l'importance de la redondance syntaxique et sémantique. Nous pourrons en effet comparer : l'entropie calculée grâce au taux de compression obtenue par ces compresseurs lexicaux, l'entropie topologique calculée par les compresseurs universels, et l'entropie "idéale" calculée par Shannon.
Nous présentons des compresseurs utilisant un transducteur déterministe en sortie. La fonction de décodage est définie par un parcours d'automate déterministe. Tous les compresseurs décrits utilisent des transducteurs définis sur l'automate du DELAF. La fonction de codage est effectuée par un parcours du transducteur ; le code émis est le texte sous forme codée. Nous décrivons plus loin la gestion des mots inconnus.
La fonction de décodage utilise le même transducteur, mais les rôles des étiquettes entrées et sorties sont inversés. Cette condition est imposée pour les raisons pratiques suivantes :
- l'utilisation d'un même objet pour le codage et la décodage simplifie la gestion et réduit l'espace utilisé ;
- la construction d'un transducteur de taille raisonnable à partir de la transduction sous forme de listes n'est pas toujours possible, comme nous l'avons vu dans le chapitre précédent .
Exemple :
Examinons un premier codeur/décodeur défini par le transducteur utilisé dans la fonction de hachage précédente (cf paragraphe 4.4.1.). Le codage effectue une transformation des mots en nombres entiers décrits sur 20 bits. Chaque mot est codé par son adresse lexicographique. Cette adresse est une position dans une liste triée dans l'ordre lexicographique.
Pour décoder un entier i, on se place sur l'état initial et on cherche la transition (q0,a,q) telle que :
Cardt((q0,a,q))= maximum(Cardt((q0,b,p)) <= i) avec b [[propersubset]] B
Le mot commence donc par la lettre a.
On réitère l'opération avec i = (i -Cardt((q0,a,q))) sur l'état q. Si i est nul nous avons décodé le mot en entier.
Ces opérations sont effectuées par le programme hach1 écrit en language C, présenté en annexe.
Dans cet exemple, notre transducteur de (dé)codage est déterministe en sortie et le problème de délai de décodage est donc résolu.
Un parcours de l'automate permet d'initialiser notre compresseur en calculant les valeurs de Carde et Cardt pour chaque état et chaque transition. Cette initialisation peut être sauvegardée.
Le codage est linéaire :
- soit le mot à coder appartient au dictionnaire ; le codage a une complexité de O(|w|) ;
- soit le mot n'appartient pas au dictionnaire. Il faut alors coder différemment, en employant un compresseur classique. Le test d'appartenance a alors une complexité de O(|w|), et le codage classique utilisé pour les mots inconnus une complexité de O(|w|).
Le décodage est sans retour arrière, le type de décodage à effectuer étant indiqué avant chaque portion de code.
En pratique nous devons gérer le problème des mots inconnus, et en particulier :
- les noms propres ;
- les mots mal orthographiés ;
- les symboles spéciaux;
- la ponctuation.
De meilleurs résultats seraient obtenus avec une analyse lexicale permettant de réduire le nombre de mots inconnus [Si 90]. Dans les transducteurs suivants, nous ajoutons des transitions sur l'état initial pour couvrir tout l'alphabet d'entrée. Les mots inconnus sont ainsi épelés grâce à ces transitions. Ce système de gestion des mots inconnus est plus amplement décrit en annexe.
Pour garder l'automate sous-jacent des sorties déterministe, nous numérotons les transitions avec un nombre de bits fixe.
Exemple :
La Figure 34. présente un transducteur, défini sur l'automate de la Figure 4., qui code les chemins dans l'automate par des groupes de bits de longueur fixe. Les transitions de l'état initial sont codées sur trois bits, les sorties sur les transitions de l'état initial sont sur trois bits les autres sur 1 bit, sauf la transitions par n dans le mot un.
Figure 34.
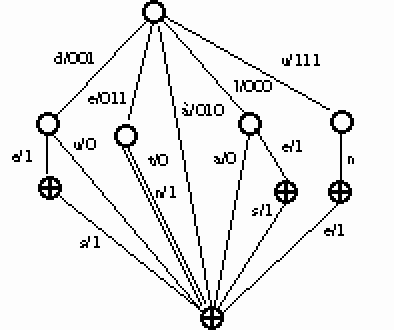
Le mot de est codé par la suite 001 1 0, le dernier zéro codant la transition terminale fictive. Le mot des est codé par 001 1 1. Le dernier état n'ayant pas de transition sortante, il n'y pas d'émission de bit. La transition qui code le n de un et une n'émet pas de bit, en effet il n'y a qu'une transition donc pas de choix à coder.
Les expériences de compression effectuées avec un tel transducteur représentant le DELAF nous donnent des résultats légèrement meilleurs que ceux des compresseurs universels, pour des textes ne contenant pas de mots inconnus. Le gain n'est pas substantiel.
Supposons dans un premier temps que tout les mots apparaissent de façon équiprobable dans le texte à comprimer. Cette hypothèse est totalement erronée en ce qui concerne une langue naturelle : le mot Æschne ("grande libellule à abdomen cylindrique" [Robert Méthodique]) est beaucoup moins fréquent que la préposition de . L'hypothèse nous permet de décrire plus simplement la méthode de construction qui sera ensuite corrigée.
Nous utilisons des arbres de Huffman. Ces arbres nous permettent de construire des codes préfixes de longueur moyenne minimum. Le code émis est réduit, et le transducteur est conservé déterministe en sortie.
Nous utilisons le code de Huffman sur chaque état pour coder les transitions. La fréquence d'utilisation d'une transition est le cardinal du langage reconnu par le sous-automate défini par l'état pointé par la transition. La probabilité est donnée par la fréquence divisée par le nombre total de mots. L'arbre de Huffman peut être fabriqué indifféremment avec des probabilités ou des fréquences.
P((q,a,p))= F(Carde(p);|L(A)|).
Figure 35.
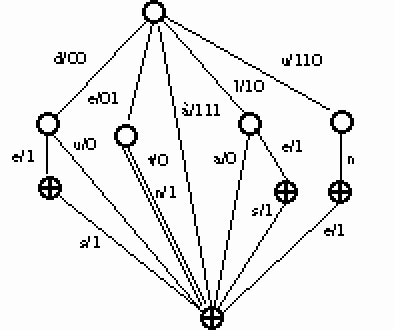
Exemple :.
Considérons le transducteur de (dé)codage de la Figure 35. Pour coder les transitions de l'état initial nous utilisons l'arbre de Huffman suivant :
Figure 36.
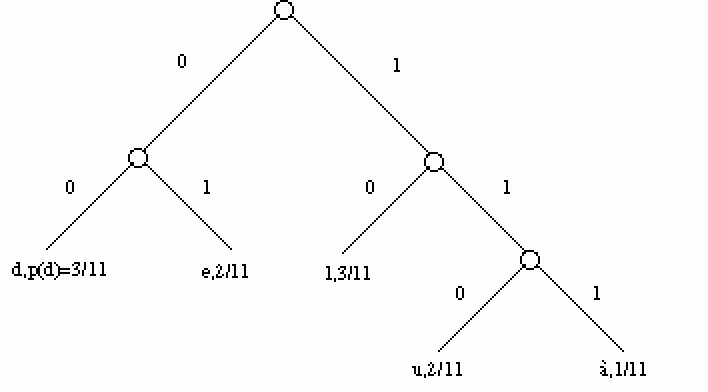
Les états terminaux sont considérés comme ayant une transition de plus, de poids 1.
Le compresseur ainsi défini ne donne pas de résultats meilleurs que le compresseur naïf. Ceci est dû aux fréquences utilisées.
Quand on effectue le codage avec ce type de transducteur défini sur le DELAF, la préposition à est codée avec plus d'un octet . On n'obtient donc pas une compression très efficace!
Nous avons à notre disposition un dictionnaire des fréquences des mots établi par Jean Baudot 1990. Il s'agit en fait d'un dictionnaire des fréquences des lemmes : toutes les formes fléchies du verbe être (suis, serait, étions,...) sont comptabilisées comme autant d'occurrences du verbe être . Nous avons besoin pour utiliser notre compresseur d'un autre dictionnaire de fréquences, qui ne tienne compte que des suites de caractères. Seule une même suite de caractères doit être considérée comme un unique mot pour le calcul des fréquences.
Remarque : les tests de compression sont effectués sur des textes n'appartenant pas au corpus. Ceci permet d'éviter d'obtenir des résultats qui serait déformés par le fait que les fréquences sont spécifiquement adaptées aux textes de notre corpus.
Pour construire le (dé)codeur nous employons la technique précédente en utilisant les nouvelles valeurs de Cardt().
Exemple :
Supposons par exemple que nos 11 mots aient les probabilités
d'apparition suivantes :
à : 0,50 (un mot du texte a
une chance sur deux d'être le mot à)
la,le,les : 0,10
un,une : 0,05
en
: 0,03
et : 0,02
de,des,du,un,une
: 0,01
Soit pour les transitions partant de l'état initial les poids suivants :
à: 0,5 ; d: 0,03 ; e: 0,05 ; l: 0,3 ; u: 0,02
ce qui nous donne les codes utilisés dans la Figure 37.
Figure 37.
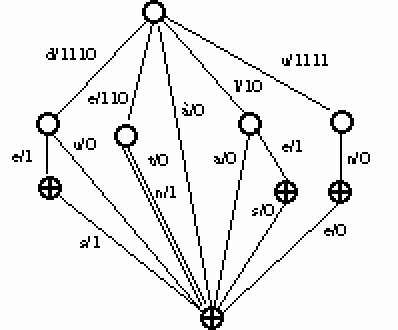
Les mots fréquents sont transformés en suites très courtes ; par exemple le mot à est codé avec un seul bit. Les mots peu fréquents sont codés par des suites plus longues.
Pour avoir une idée précise de la fréquence des mots, il nous faudra utiliser de très grands corpus de textes.
Les résultats déjà obtenus sont très intéressants. Sur des textes comportant 16 signes de ponctuations et pas de mots inconnus, les résultats sont excellents : un taux de 0.3 est courant. Pour étendre ce résultat à des textes comportant une proportion normale de mots inconnus, un mécanisme d'analyse lexicale doit être employé afin d'éliminer les cas de non-reconnaissance dus à des phénomènes typographiques comme les majuscules, les signes de ponctuation ou des objets tels que des nombres écrit en alphabet romain ou arabe. Ces problèmes sont traités dans [Si.90].
Pour ne pas avoir à coder l'adaptativité dans le code nous avons choisi le principe suivant: l'adaptation des fréquences ne se fait qu'après le codage d'un mot.
Les mots inconnus font l'objet d'une gestion indépendante, qui peut également être adaptative. Par exemple les noms propres méritent une gestion spéciale : il est très fréquent qu'un même nom propre apparaisse plusieurs fois dans un texte donné.
Pour les mots connus, on calcule pour chaque état l'arbre de Huffman des transitions grâce aux fréquences de celles-ci, comme dans le compresseur à délai 1 précédent. Ensuite quand on avance sur la transition sélectionnée, on incrémente sa variable Cardt de 1. Ainsi au passage suivant sur le même mot la fréquence a augmenté. Progressivement, plus le mot est utilisé plus la longueur du code émis diminue.
Ce compresseur adaptatif recalcule un arbre de Huffman sur chaque état. Ceci est théoriquement assez coûteux : O(|B|) pour chaque état ; mais en fait c'est raisonnable en pratique, car les états de l'automate du DELAF ont en moyenne moins de 3 transitions. L'état initial qui, lui, a beaucoup de transitions fait l'objet d'une gestion spécifique utilisant par exemple le code de Huffman adaptatif.
Exemple :
Le dictionnaire utilisé contient 8 mots équiprobables {ab,açaa,bab,bba,bbb,bca,bcb}. Ces mots peuvent donc êtres codés sur trois bits. Or le transducteur à délai 1 en sortie de la Figure 38. émet un code de 2 bits pour les mots aa et ab et un code de 4 bit pour les autres. La longueur moyenne du code émis est donc plus longue que celle du code généré sur trois bits.
Figure 38.
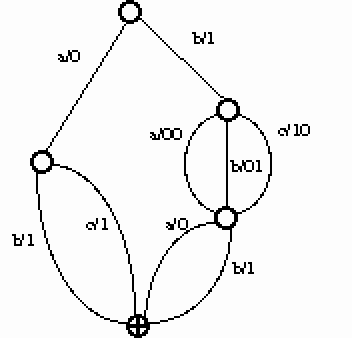
Il est possible, avec un transducteur à délai 2 en sortie, d'émettre ce code sur trois bits, ce que fait le transducteur suivant :
Figure 39.
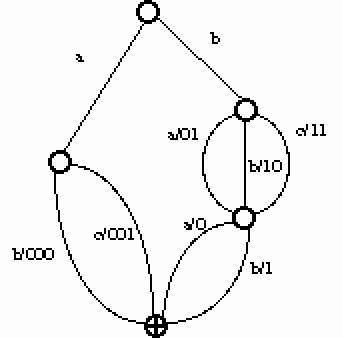
Nous avons ici un alphabet de 8 lettres équiprobables (les 8 mots). Les probabilités d'apparition de ces mots sont des puissances entières de F(1;2). Ce qui est la condition d'optimalité du codage de Huffman dans les codages par substitution ( cf. [AHU-87] ).
Cet exemple présente donc un cas où le codage de Huffman effectué sur les mots est optimal.
Nos compresseurs précédents, en effet, ne sont pas optimaux, puisque sur chacun de nos états, si les Cardt ne génèrent pas des probabilités qui sont des puissances entières de F(1;2), une émission superflue est effectuée. Pour obtenir une émission plus efficace, nous grouperons quand c'est possible les transitions de façon à ce que, dans chaque groupe, la somme des probabilités des transitions soit une puissance entière de F(1;2).
Le délai de décodage doit rester borné, ce qui est assuré si les codes définissent tous des chemins distincts dans l'automate sous-jacent des sorties. L'algorithme de construit effectue cette opération uniquement si les états buts des transitions regroupées sont de degré entrant 1, n'ayant qu'un seul prédécesseur. Des recherches en cours tendent à améliorer cet algorithme, mais de nombreux problèmes apparaissent alors pour construire de façon simple le décodeur. Les problèmes soulevés dans la section 4 concernant la construction de transducteurs de taille raisonnable restent ouverts. La taille du transducteur représentant [[Gamma]]-1 est trop importante.
La difficulté réside dans le choix des chaînes de caractères à introduire dans le dictionnaire, et dans la façon de découper les textes pour en extraire ces chaînes. Une approche par longueur, consistant à regarder les fréquences des suites de n caractères, ne permet pas d'accéder à l'information fondamentale : " les textes d'une langue naturelle sont écrits presque exclusivement avec des mots de cette langue" .
L'algorithme de minimisation s'applique à un automate normalisé où les états sont tous accessibles et coaccessibles.
Pour obtenir un automate normalisé, il suffit de faire un parcours de l'automate qui élimine les états non-accessibles et les états non-coaccessibles. L'algorithme effectue un parcours pour calculer la hauteur des états. Ce parcours permet du même coup de normaliser l'automate.
La minimisation d'un automate consiste à éliminer les états équivalents. Deux états sont dis équivalents si ils ont le même langage associé. Le langage associé à l'état s est le langage reconnu par l'automate normalisé où s est l'état initial. Dans la Figure 31. nous présentons l'automate normalisé associé à l'état s A=(Q,B,F,T,s) ; le langage reconnu est {n,ne}.
Figure 40.
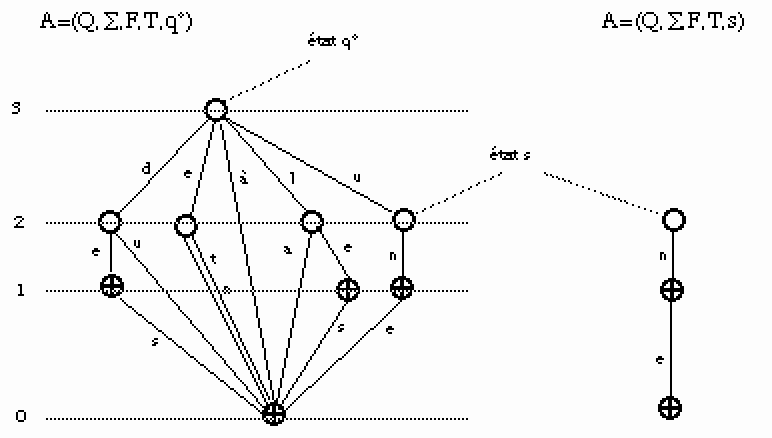
Définitions :
Nous dirons de deux états qu'ils sont distingués si ils ne sont pas équivalents ; et d'un ensemble d'états qu'il est distingué quand tous les états qu'il contient sont deux à deux distingués.
Soit s un état de Q, la hauteur h de s est définie par :
h(s)=max{|w| tel que s.w [[propersubset]] [[Tau]]}
en d'autres termes, la hauteur de s est la longueur du plus long mot du langage de l'automate associé à s.
Dans un automate comportant des cycles, tous les états appartenant à un cycle sont de hauteur infinie, la notion n'a plus d'intérêt.
La fonction Hauteur est une application. Elle défini une partition de l'ensemble des états.
Nous noterons [[Pi]] cette partition par hauteurs et [[Pi]]i le sous-ensemble des états de hauteur i.
Pour le calcul de la partition [[Pi]] , nous utilisons une fonction récursive qui parcourt l'automate :
fonction Hauteur(s : état) : entier;
var hc : entier; t
: transition;
début
si s->hauteur > 0
alors Hauteur := s->hauteur;
sinon
début
hc:=0;
pour toutes les transitions t de s faire
début
hc=max(hçauteur(t->but));
fin;
Hauteur:= hc; Ajouter s à [[Pi]]hc
fin;
fin;
Propriété des hauteurs.
Si tous les [[Pi]]j pour j<i sont distingués alors deux états p et q de [[Pi]]i sont équivalents si et seulement si ils sont tous deux terminaux ou tous deux non-terminaux et [[universal]] a [[propersubset]] B on a p.a=q.a .
Cette propriété nous fournit une méthode rapide et simple pour calculer l'équivalence de deux états, et nous permet d'écrire l'algorithme suivant :
Minimisation:
calculer [[Pi]]
pour i:= 0 à
Hauteur(q0) faire
début
Trier les états de
[[Pi]]i par leurs transitions et leur terminalité.
fusionner tous les
états équivalents.
fin.
Théorème 1.
En utilisant un algorithme de tri d'une complexité de O(f(n)), l'algorithme ci-dessus minimise un automate acyclique normalisé avec une complexité en O(iSU(i;;f(|[[Pi]]i|))).
La complexité totale est de O(|F|+iSU(i;;f(|[[Pi]]i|)).
Preuve : la propriété des hauteurs nous assure que l'algorithme fournit bien l'automate minimal. La partition [[Pi]] est élaborée par un parcours de l'automate, chaque transition n'étant utilisée qu'une fois. Le tri est effectué une seule fois sur chaque élément de la partition. Le calcul de complexité est direct.
Remarque : la partition initiale [[Pi]] peut être raffinée en séparant les états terminaux [[Pi]]T des non terminaux [[Pi]]NT. Les tris s'effectent sur les deux éléments [[Pi]]Ti et [[Pi]]NTi à chaque hauteur. Ceci accélère l'algorithme dans le cas où la fonction f n'est pas linéaire. Nous utiliserons cette remarque dans l'algorithme final, car elle simplifie la mise en oeuvre.
Le tri lexicographique utilise répétitivement le tri par sélection de place.
Si l'on suppose que l'ensemble des objets que l'on cherche à trier est dans un intervalle défini, une méthode de tri assez naturelle est de positionner un à un les objets à leur place respective, comme le fait un facteur qui trie du courrier. Celui-ci a une boîte pour chaque département (l'intervalle de variation), il y place une à une les lettres en fonction du département indiqué.
Plus formellement :
soit la séquence à trier a1,a2, ...,an d'entiers de l'intervalle [1,m]
1. On crée un tableau TI de m listes vides
2. On parcourt la séquence en plaçant chaque entier ai dans la ai-ème liste
3. La liste triée résulte de la concaténation dans l'ordre 1 à m des listes non vides de TI.
Cet algorithme utilise n étapes pour parcourir la liste, et m étapes pour concaténer les listes. Soit une complexité en O(n+m).
Le principe du tri lexicographique sur les mots consiste à appliquer ce tri par sélection de place sur les lettres successives des mots à trier.
Soit la séquence de mots de longueur l sur un alphabet à m lettres A1,A2, ...,An ;
on suppose qu'initialement la séquence est dans la liste S.
1. On crée un tableau TI de m listes vides
2. Pour i variant de l à 1 :
3. on parcourt la séquence S en plaçant le mot A dans la ai liste de TI
4. on concatène les listes de TI dans S
5. La liste S obtenue est la séquence triée lexicographiquement.
Exemple :
Trions les mots {baa,baçbçab,abçaa} sur l'alphabet [a,b,c].
Le premier tri, en fonction de la troisième lettre, crée les listes :
(baa,aaa ; aab ; baçbçbc)
puis en fonction de la deuxième lettre :
(baa,aaa,aab,bac ; abçbc)
puis en fonction de la première lettre :
(aaa,aab,abçbc ; baa,bac)
A chaque tri par sélection de place l'ordre des tris précédents est conservé, notre séquence est donc triée après le dernier tri sur la première lettre.
Remarque : on peut trier des mots de longueur variable en rajoutant à l'étape 3 les mots de longueur i au début de la liste S. Ceci suppose que nous connaissions, ou calculions, la longueur des chaînes.
La complexité de cet algorithme est O(l(n+m)). On effectue l tris par sélection de place de n entiers dans un intervalle [1,m]. Remarquons que l'algorithme procède de droite à gauche et parcourt complètement l'ensemble de mots.
Pour notre minimisation nous ne cherchons pas à trier mais à partitionner notre séquence en sous-ensembles de mots identiques. Il suffit donc de regarder les préfixes communs des mots de notre séquence, c'est ce qui est mis en oeuvre dans l'algorithme suivant.
Nous utilisons une structure de donnée nouvelle : la super-liste, qui est une liste de listes. Trois variables sont de ce type : Q1 Q2 et EGAUX.
L'entrée est une séquence A1,A2, ...,An de mots sur un alphabet à m lettres.
On suppose que la séquence est initialement dans une liste placée dans la super-liste Q2.
Tant que Q2 != Ø faire
Déplacer
Q2 dans Q1 ; i := i +1;
Tant que Q1 != Ø
faire
soit L la première liste de Q1;
Tant
que L != Ø faire
soit A le premier mot de
L
(B) si A est de longueur i Ajouter A
à égaux
sinon Ajouter A à
TI[ai]
(* ou TI est un tableau chaîné voir ci-dessous
*)
fin de tant que
(A) Ajouter TI à la super
liste Q2
Ajouter égaux à EGAUX
fin de tant que
fin de tant que
La super-liste EGAUX contient les listes de mots identiques.
Ajouter un mot dans TI prend un temps constant ; recopier TI dans Q2 prend un temps proportionnel aux nombre de listes TI non vides. Les listes réduites à un élément sont purement et simplement oubliées à la recopie.
Théorème 2 :
L'algorithme précédent sépare une séquence de mots de longueur variable finie, où chaque lettre est un nombre entier compris entre 1 et m, en un temps O(p') où p' est la longueur totale des préfixes communs des mots séparés. La mémoire additionnelle nécessaire est O(n+m).
Preuve : on démontre que l'algorithme se termine en un temps O(p') par induction sur le nombre d'itérations de la boucle la plus extérieure. L'hypothèse d'induction est qu'après i exécutions de cette boucle, les listes de Q2 sont toutes faites de mots comportant un préfixe identique de longueur i.
Dans la boucle la plus profonde une liste L est séparée en fonction du i-ème caractère de chaque mot, ce qui crée une ou plusieurs listes où le i-ème caractère est constant. Les listes rajoutées après la boucle intérieure vérifient donc la propriété d'induction. Comme la boucle intérieure est effectuée sur toutes les listes de Q1, notre hypothèse tient.
La ligne (A) s'effectue en un nombre d'étapes au pire égal au nombre d'étapes effectuées par (B) (une liste est créée pour chaque mot). La complexité dépend donc de la ligne (B), exécutée une fois pour chaque lettre appartenant à un préfixe commun de notre ensemble de mots.
La mémoire additionnelle est l'espace utilisé pour TI, soit O(m), et une liste et une super-liste pour chaque mot, soit O(n).
Le plus long préfixe de deux mots a une longueur au plus égale à la longueur du plus petit mot. Les mots étant de longueur finie, notre hypothèse d'induction nous assure que l'algorithme se termine.
Nous allons utiliser l'algorithme de séparation pour extraire les listes d'états équivalents.
Pour pouvoir appliquer l'algorithme de tri, les états doivent être organisés comme des chaînes de caractères, ceci est fait en étiquetant les états par les n-uplets :
( l1,b1,l2,b2,...,ln,bn)
les li sont les lettres qui étiquètent les transitions dans l'ordre lexicographique, et les bi les numéros des états pointés par les transitions.
Cette représentation permet d'effectuer le tri. Or la longueur de ces chaînes de caractères est au maximum égale à |B|(1+log n) . C'est à dire une transition pour chaque lettre de l'alphabet, chaque transition utilisant un caractère pour la lettre et log n caractères pour la représentation en octet d'un numéro d'état. Ce log apparaît dans la complexité finale de l'algorithme, ce que nous voulons éviter, d'où le système de renumérotation suivant.
Renumérotation des états.
A chaque tri (un tri par hauteur) les états utilisés sont renumérotés au moyen d'un couple (i,num). Ce couple indique que l'état a été renuméroté pour le tri de hauteur i et que le numéro num lui a alors été affecté.
L'intérêt de cette renumérotation est que num reste borné par le nombre de transitions des états de hauteur i.
La fonction suivante renumérote l'état e pendant le tri des états de hauteur h. La variable n contient le dernier numéro utilisé ; cette variable est initialisée à zéro avant chaque tri.
fonction numéroter(e,h,n)
début
si
(e->i != h) alors
{e->i := h; e->num := n; n :=
n+1;}
retour (e->num);
fin;
Proposition : la valeur maximale que peut prendre la variable n est au plus Ei. Ei est la somme des transitions des états de hauteur i.
Preuve : la valeur maximale de n est le nombre maximal d'états auquels on peut affecter une nouvelle valeur, au plus un état pour chaque transition utilisée dans le tri des états de hauteur fixée. Chaque transition est utilisée au plus une fois par l'algorithme de tri.
Cette numérotation permet d'utiliser un tableau de Taille Ei pour effectuer le tri par sélection de place. On peut donc appliquer un tri lexicographique standard avec une complexité en O(Ei ) et non plus O(Ei log(|Q|)). Avec l'algorithme de séparation, cette technique de renumérotation ne fait que réduire la taille des tableaux TI utilisés.
Notre algorithme devient finalement :
Calculer h pour touts les états et créer les listes
[[Pi]]i
fusionner les états de [[Pi]]0 (qui sont
trivialement équivalents ).
pour i:= 1 à h(q0)
-1 faire
début
placer [[Pi]]i dans la liste
QUEUE2 (1)
i:=0;
faire
déplacer QUEUE2 dans
QUEUE1; i:=i+1;
tant que QUEUE1 non vide faire
début
soit L la première liste de QUEUE1
tant que L non vide faire
début
soit S
le premier état de L
placer S dans la position p =
renuméroter(Q[ai]) du tableau TI
(où ai est le
ième élément du label de S)
fin
ajouter (la concaténation des listes de TI non réduites
à un élément ) à QUEUE2
éliminer les
listes réduites à un élément.
fusionner les
états de TI[$]
fin.
tant que QUEUE2
non vide
fin.
Une mise en oeuvre de cet algorithme écrite en langage C, où l'on partitionne les états par hauteur et par terminalité.a donnée les meilleurs resultats. La renumérotation fait double emploi : elle permet également de redéfinir les transitions vers des états fusionnés.
Ce bon résultat de complexité permet de fabriquer un automate du DELAF raisonablement vite : une première version de la minimisation réalisée en utilisant le quicksort optimisé de la librairie UNIX nous a permis de faire une comparaison honnête, la nouvelle méthode de tri s'est avérée 100 fois plus rapide.
Dans le cas de dictionnaires où l'ensemble des informations associées aux mots est réduit, les automates à multi-terminaux fournissent un bon compromis espace / vitesse.
Dans le cas de dictionnaires complexes, où les données sont associées de façon bijective aux mots, on choisira le transducteur de hachage quand la vitesse d'accès au dictionnaire est primordiale. Si la gestion de l'espace prime sur la vitesse, l'utilisation de L'ALG interne sera préférée.
La représentation du lexique-grammaire par des automates acycliques est envisagable si une application le demande. On peut considérer le Lexique-grammaire comme une liste de mots écrits sur un alphabet de symboles comme : N0 , "se", "livre" , V ; représentant des parties du discours ou des mots.
Les systèmes de compression décrits permettent de mieux cerner la notion d'entropie d'une langue naturelle. Nous disposons maintenant de trois techniques pour estimer l'entropie d'un texte, grâce au taux de compression obtenus avec différentes méthodes. L'entropie dite topologique utilise uniquement des redondances formelles internes au texte. Elle est estimée par les taux de compression obtenus par des algorithmes comme celui de Ziv et Lempel. Le taux de compression est de l'ordre de 0,5. L'entropie lexicale est celle estimée avec nos nouveaux compresseurs ; le taux obtenu est de l'ordre de 0,3. Enfin l'entropie estimée par Shannon permettrait d'atteindre un taux de 0,1. Les différences entre ces entropies s'expliquent simplement. Plus on dispose d'informations concernant la structure du texte, plus il devient facile de le comprimer.
L'expérience de Shannon a estimé l'entropie de textes écrits sur un alphabet de 27 lettres. Il serait intéressant de refaire l'expérience sur des textes écrits sur un alphabet comportant l'ensemble des caractères de ponctuation, comportant des mots inconnus comme des noms propres, ou sur des textes écrits dans un langage spécialisé (scientifique, artistique, etc.).
Enfin un compresseur efficace devra utiliser des techniques d'analyse lexicale et/ou syntaxique : le nombre des mots considérés comme connus pourrait être amélioré, et l'utilisation d'informations concernant la structure des phrases permettrait une compression plus importante.
Pour ces compresseurs, les transducteurs sont la structure de données adéquate.
[AHU 87] A.V. AHO, J.E. HOPCROFT, J.D. ULLMAN, Structures de Données et Algorithmes, InterEditions, (1987).
[AHU 87] A.V. AHO, J.E. HOPCROFT, J.D. ULLMAN, Traduction en français du précédent.
[An 79] D. ANGLUIN, Inference of Reversible Languages, J.A.C.M. Vol.29, No.3, July (1982). pp 741-765.
[An 80] D. ANGLUIN, Inductive inference of formal languages from positive data, Inf. Control. 45, (1980).
[ASU 86] A.V. AHO, R. SETHI, J.D. ULLMAN, Compilers - Principles, Techniques and Tools, Addison-Wesley, Reading, Mass., (1986). Traduit en Francais: Compilateurs - principes, techniques et outils, InterEditions (1989).
[Ba 88] S. BAASE, Computer Algorithms - Introduction to Design and Analysis, Addison-Wesley, Reading, Mass., (1988). 2nd edition.
[Be 79] J. BERSTEL, Transductions and context-free languages, Teubner Studienbücher Informatik, (1979).
[Bl 72] M. BLUM, R.W. FLOYD, V.R. PRATT, R.L. RIVEST, AND R.E. TARJAN "Time bounds for selection". J. computer and system sciences 7:4, (1972).pp.448-461
[BP 85] J. BERSTEL, D. PERRIN, Theory of codes, Academic Press, Orlando, Florida, (1985).
[Br 86] R.E. BRYANT, Graph-based algorithms for boolean function manipulation, IEEE Transactions on Computers, Vol. C-35, ndeg.5, (1986). pp.677-691.
[CC 82] A. CARDON , M. CROCHEMORE, Partitioning a graph in O(|A|log2|V|), Theoret. Comput. Sci., 19, (1982). pp.85-98.
[CH 87] G.V. CORMACK, R.N.S. HORSPOOL, Data Compression Using Dynamic Markov Modelling, Comput. J. 30,6, (1987). pp.541-550.
[Co 71] S.A. COOK, Linear time simulation of deterministic two-way pushdown automata, Information Processing 71, (1972). pp.75-80.
[Co 84] B. COURTOIS, Le dictionnaire des formes simples du français. Notice technique, Rapport de recherche du LADL, université Paris 7, (1984).
[Co 90] B. COURTOIS, M. SILBERZTEIN, "Dictionnaires électroniques du français. Présentation", Langue Française. 87. Larousse. (1990).
[Cr 72] C.A. CRANE, "linear lists and priority queues as balanced binary trees," Ph.D. Thesis, STanford University, (1972).
[Cr 86] M. CROCHEMORE, Transducers and repetitions, Theoret. Comput. Sci. 45, (1986). pp.63-86.
[Cr 89a] M. CROCHEMORE, Data compression with substitution, in: (M. GROSS, D. PERRIN, editors, Electronic Dictionaries and Automata in Computational Linguistics, Lecture Notes in Computer Science 377, Springer-Verlag, Berlin, (1989). pp.1-16.
[Cr 89b] M. CROCHEMORE, Automata and algorithms, in: (J-E. PIN, editor, Formal Properties of Finite Automata and Applications, Lecture Notes in Computer Science 386, Springer-Verlag, Berlin, (1989). pp.166-175.
[CZ 89] M. CROCHEMORE, M. ZIPSTEIN, Transducteurs arithmétiques, Rapport L.I.T.P. 89-12, Université Paris 7, (1989).
[EGGI 90] D. EPPSTEIN, Z. GALIL, R. GIANCARLO, G. ITALIANO, Sparse dynamic programming, J. ACM, (1990). à paraître.
[Fa 73] N. FALLER, An adaptive system for data compression, in Record of the 7th Asilomar Conference on Circuits, Systems, and Computers, (1973). pp.593-597.
[Fl 73] R.W. FLOYD, R.L. RIVEST "Expected time bounds for selection" Computer Science Dept., Standford University, (1973)
[Ga 78] R.G. GALLAGER, Variations on a theme by Huffman, I.E.E.E. Trans. Inform. Theory IT 24,6, (1978). pp.668-674.
[GP 89] M. GROSS, D. PERRIN, editors, Electronic Dictionaries and Automata in Computational Linguistics, Lecture Notes in Computer Science 377, Springer-Verlag, Berlin, (1989).
[Gu 90] A. GUILLET, "Reconnaissance des formes verbales avec un dictionnaire minimal". Langue Française. 87, Larousse, (1990)
[He 87] G. HELD, Data Compression - Techniques and Applications, Hardware and Software Considerations, John Wiley & Sons, New York, NY, (1987). 2nd edition.
[HK 71] J.E. HOPCROFT & R.M. KARP, An algorithm for testing equivalence of finite automata,TR-71-114, dept of computer Science,Cornell Univ, (1971) Voir [Ah-74] pp143-145 pour une description.
[Ho 73] J.E. HOPCROFT, J.D. ULLMAN, "Set merging algorithms" SIAM J. computing 2:4, (1973). pp.294-303.
[HPS-91] HANSEL, D. PERRIN, SIMON, la compression , manuscrit.
[HU 79] J.E. HOPCROFT, J.D. ULLMAN, Introduction to automata, languages and computation, Addison-Wesley, Reading, Mass, (1979).
[Hu 51] D.A. HUFFMAN , A method for the construction of minimun redundancy codes, Proc. IRE 40, (1951). pp.1098-1101
[Hu-54] D.A. HUFFMAN, The synthesis of sequential switching machines, J. Franklin Inst. 257, (1954).
[Kn 73] D.E. KNUTH The art of computer programming, Vol 3, Sorting and Searching. Addison Wesley Pu. Co. Reading,MA,(1973).
[Kn 85] D.E. KNUTH, Dynamic Huffman coding, J. Algorithms 6 (1985) pp.163-180.
[La 88] E. LAPORTE, Méthodes algorithmiques et lexicales de phonétisation de textes. Applications au français, thèse de doctorat, Université Paris 7, (1988).
[Li 83] F.M. LIANG, Word Hy-phen-a-tion by Com-pu-ter, PhD Thesis, Computer Science Departement, Standford University, Research Report STAN-CS-83-977, (1983)
[LZ 76] A. LEMPEL, J. ZIV, On the complexity of finite sequences, I.E.E.E. Trans. Inform.Theory IT 22,1, (1976). pp.75-81.
[McI 81] D. MCILROY, Development of a spelling list. IEEE transactions on communications, vol. com-30, ndeg. 1, (1981).
[Mi-67] M. MINSKY, Compilation, Finite and infinite Machines, Prentice Hall, Englewood diffs, N.J, (1967).
[Mo 56] E.F. MOORE, Gedanken experiments on sequentieals machines Automata studies Princeton Univ.Pres, (1956). pp129-153.
[Mo 68] D.R. MORRISON, PATRICIA - practical algorithm to retrieve information coded in alphanumeric, J. ACM 15, (1968). pp.514-534.
[Ni 81] R. NIX, Experiences with a space efficient way to store a dictionnary CACM 24,may, (1981).
[RS 59] M.O. RABIN, D. SCOTT, Finite automata and their decision problems IBM.J. Research and Development 3, (1959). pp.114-125.
[Se 88] R. SEDGEWICK, Algorithms, Addison-Wesley, Reading, Mass, (1988). 2nd edition.
[Sh 51] C.E. SHANNON, Prédiction and Entropy of Printed English, Bell system Technical Journal 3:50-64 (1951) [reproduit dans Key papers in the development of information theory].
[Si-90] M. SILBERZTEIN, Dictionnaires électroniques et reconnaissance lexicale automatique, Thèse de doctorat, Université Paris 7, (1990).
[St 77] J.A. STORER, NP-completeness results concerning data compression, Report 234, Princetown University, (1977).
[Tr 75] R.E. TARGAN On the efficiency of a good but not linear set merging algorithm,JACM 22, (1975). pp.215 -225
[TY 79] R.E. TARJAN, A.C. Yao storing a sparce table. Comm. ACM, 22:606-611, (1979).
[We 84] T.A. WELCH, A technique for high-performance data compression, I.E.E.E. Computer 17,6, (1984). pp.8-19.
[Zip 90] M. ZIPSTEIN, Les méthodes de compression de textes, algorithmes et performances, Thèse de Doctorat Université PARIS VII, (1990), Rapport Technique 90.19, Laboratoire d'informatique Théorique et Programation, Paris 1990.
[ZL 77] A. LEMPEL, J. ZIV, A Universal algorithm for sequential data compression, I.E.E.E. Trans. Inform.Theory IT 23,3, (1977). pp.337-343.
[ZL 78] A. LEMPEL, J. ZIV, Compression of individual sequences via variable length-coding, IEEE Trans. Inform. Theory 24, (1978). pp.530-536.
Pour les degrés supérieurs à 7, le pourcentage est inférieur à 1%.
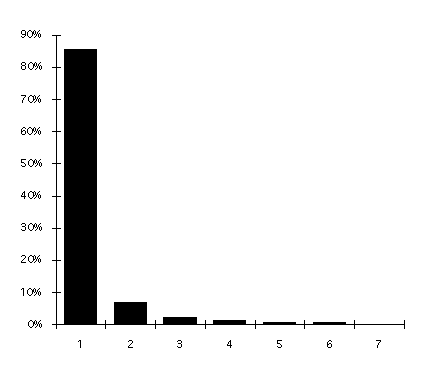
Les plus grands degrés entrants sont en ordre décroissant : 5600, 3868, 3622, 3399, 3379, 3043, 2275, 1987, 1252.
On remarque que 85,5 % des états sont de degré entrant 1. Si l'on regarde uniquement les états qui sont dans l'ALG interne, nous ne trouvons plus que 28513 états (58%) auxquels on accède par un chemin unique.
Le graphique suivant nous donne une idée de la qualité de l'ALG interne en tant que fonction de hachage. L'ALG interne fournit pour chaque mot une adresse qui dépend du plus long préfixe du mot qui est dans l'ALG interne. Ce plus long préfixe est partagé avec d'autres mots, le nombre de ces mots est noté cardinal du noeud.
Répartition des cardinaux des langages reconnus par les sous-automates engendrés par les états qui sont des noeuds de l'ALG interne de l'automate du DELAF. On trouve en ordonnée le nombre de noeuds, en abscisse le cardinal .