Minesweeper (récursivité)

On souhaite écrire une version du jeu Minesweeper (démineur). On utilise la librairie MLV pour gérer le graphisme et les interactions avec l'utilisateur. Normalement, la librairie est disponible sur vos comptes de l'université; si vous souhaitez l'utiliser sur votre ordinateur personnel, vous pouvez vous référer à cette page. Commencer par récupérer l'archive Sweeper.zip et extraire les fichiers dans votre répertoire de travail.

$ make
gcc -c -o sweeper.o sweeper.c -Wall -ansi
gcc -c -o grid.o grid.c -Wall -ansi
gcc -c -o draw.o draw.c -Wall -ansi
gcc -o sweeper sweeper.o grid.o draw.o -lMLV -lm -lSDL
$ ./sweeper

Vous voyez qu'il y a déjà une partie du jeu en place mais que le jeu ne fonctionne pas. Plus précisément, il manque une fonction qui place les mines sur la grille initiale et une fonction qui découvre les cases dès que le joueur clique (gauche) sur une case. Familiarisez-vous avec les structures cell et grid, les fonctions pour dessiner la grille et la fonction principale du jeu.

Écrire la fonction void add_mines(grid *g, int n) dans grid.c. La fonction prend (un pointeur vers) une grille, g, et un entier n et elle doit ajouter exactement n mines sur la grille à des emplacements choisis de facon aléatoire. De plus, cette fonction doit mettre à jour les champs mine_count des cases voisines des mines. Voir la figure ci-dessous : 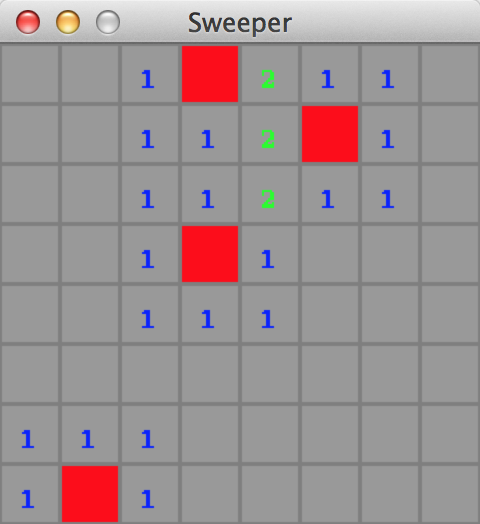Pour vérifier votre fonction, vous pouvez ajouter dans votre main un appel à la fonction set_all_visible(g). Cette fonction rend toutes les cases visibles. N'oubliez pas d'enlever cet appel avant de commencer l'exercice suivant.

Écrire la fonction int uncover(grid *g, cell *c) dans grid.c. La fonction prend (un pointeur vers) une grille, g, et une case, c. Elle doit renvoyer le nombre de cases qui ont été découvertes. Pour cela, elle doit découvrir récursivement les cases comme suit :

1. Si la case est déjà visible ou marquée (gris-sombre, par un clic droit), alors la fonction ne découvre pas la case courante, ni les cases voisines. Elle renvoie 0 pour indiquer qu'aucune case n'a été découverte.
2. Sinon, on commence par découvrir la case c et on utilise la fonction draw_cell_actualise_window(c) pour visualiser ce changement.
   1. Si la case c contient une mine ou si son compteur de mines voisines ne vaut pas 0, alors on renvoie 1 pour indiquer qu'une seule case a été découverte.
   2. Sinon, on lance, pour chaque voisin v tel que v n'est pas découvert, un appel récursif à uncover sur v. On récupère les résultats (nombre de cases découvertes) de tous les appels et on renvoie leur somme (+ 1 pour la découverte de la case c).

Pour mieux voir l'ordre dans lequel les cases sont découvertes, vous pouvez utilisez la fonction void MLV_wait_milliseconds(int milliseconds) de la librairie MLV.

Implanter la fonction récursive pour la résolution du puzzle N reines vue au cours. Comparer le nombre de solutions obtenu avec les valeurs tabulées sur le lien suivant : The On-Line Encyclopedia of Integer Sequences.

1. Pour quelles valeurs de N pouvez-vous obtenir le nombre de solutions dans un temps raisonnable ?
2. Implanter au moins une des améliorations suivantes :
   
   • Ajouter une visualisation des solutions du puzzle en utilisant la librairie MLV.
   • Ajouter une visualisation de la recherche en utilisant la libraire MLV. C'est-à-dire, dans chaque appel de la fonction récursive, vous dessinez l'échiquier avec les reines qui sont déjà placées et les cases potentielles pour le placement de la prochaine reine.
   • Trouver des optimisations de votre fonction afin d'obtenir le nombre de solutions pour une plus grande valeur de N.