:: Enseignements :: ESIPE :: E4INFO :: 2008-2009 :: Algorithmique ::
Est-il possible de dessiner les graphes suivants sans lever le crayon?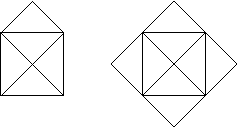
C'est le problème du chemin eulérien. Dans ce TP, on va écrire un programme qui le résout.
![[LOGO]](http://igm.univ-mlv.fr/ens/resources/mlv.png) | Parcours eulérien |
Est-il possible de dessiner les graphes suivants sans lever le crayon?

C'est le problème du chemin eulérien. Dans ce TP, on va écrire un programme qui le résout.
Exercice 1 - Graphes non orientés
Réutiliser l'implémentation des graphes par liste d'adjacence pour
implémenter les graphes non orientés et sans poids. On veut pouvoir
- ajouter une nouvelle arête,
- la supprimer.
Exercice 2 - Calculer le degré
On va utiliser le théorème suivant, dit théorème d'Euler : "il
existe un chemin eulérien si et seulement si il y a 0 ou 2 sommets
de degré impair". Implémenter une fonction qui renvoie le nombre de
sommets de degré impair.
Que se passe-t-il s'il n'y a qu'un seul sommet de degré impair?
Que se passe-t-il s'il n'y a qu'un seul sommet de degré impair?
Exercice 3 - L'algorithme d'Euler
Pour trouver un chemin eulérien, on applique l'algorithme
suivant.
- compter le nombre de sommets de degré impair,
- Si
- c'est 0 : construire un cycle partant du premier sommet,
- c'est 2 : construire un chemin entre les deux sommets en question,
- sinon, il n'y a pas de chemin eulérien.
- parcourir le chemin déjà construit : à chaque sommet
- tant qu'il reste des arêtes partant de ce sommet dans le graphe, construire un cycle partant de ce sommet et l'insérer dans le chemin.
Etant donné les conditions sur le graphe, construire un chemin ou un
cycle n'est pas compliqué : il suffit de partir de l'origine, de
prendre la première arête rencontrée et de recommencer récursivement.
Se convaincre que c'est vrai, puis écrire la fonction qui :
Se convaincre que c'est vrai, puis écrire la fonction qui :
- renvoie un chemin entre deux sommets de degré impair dans un graphe eulérien,
- renvoie un cycle partant d'un sommet de degré pair dans un graphe eulérien dont tous les sommets sont de degré pair;
Ecrire l'algorithme de recherche de chemin eulérien.
© Université de Marne-la-Vallée
