:: Enseignements :: ESIPE :: E4INFO :: 2008-2009 :: Algorithmique ::

Composantes connexes

Dans un graphe non orienté, une composante connexe est un sous-graphe induit maximal connexe, c'est-à-dire un ensemble de points qui sont reliés deux à deux par un chemin. On peut ainsi regrouper les sommets d'un graphe selon leur appartenance à la même composante connexe.
Dans le cas des graphes orientés on parle de composante fortement connexe pour un ensemble de sommets reliés les uns aux autres par des chemins du graphe.
Dans ce TP on va calculer les composantes (fortement) connexes d'un graphe.

Exercice 1 - Dans un graphe non-orienté

Modifier la structure de graphe pour intégrer le coloriage des sommets.

Pour les distinguer les composantes connexes les unes des autres, chaque sommet se verra attribuer une couleur; deux sommets de même couleur seront dans la même composante.
Ecrire une fonction CC_sommet(G,x,i) qui colorie la composante connexe d'un sommet x avec la couleur i :

colorier x avec i
pour tout sommet y successeur de x
  si y n'est pas colorié faire CC_sommet(G,y,i)

Ecrire une fonction CC(G) qui colorie toutes les composantes connexes d'un graphe avec une couleur par composante :

tant que tous les sommets de G ne sont pas coloriés
  choisir un sommet x non colorié
  choisir une nouvelle couleur i
  CC_sommet(G,x,i)

Exercice 2 - Dans un graphe orienté, version naïve

Deux sommets x et y du graphe sont dans la même composante fortement connexe si et seulement si il existe un chemin de x à y (y est accessible depuis x) et un chemin de y à x (x est accessible depuis y). D'où l'idée suivante d'algorithme :

pour tout sommet x calculer la liste Acc(x) des sommets accessibles depuis x
pour tout sommet x
  pour tout sommet y dans Acc(x)
    si x est dans Acc(y) alors colorier x et y de la même couleur

Ecrire l'algorithme naïf qui calcule les composantes fortement connexes d'un graphe orienté. Quelle est sa complexité ?

Exercice 3 - Dans un graphe orienté

Il existe plusieurs algorithmes efficaces, et tous utilisent des parcours de graphes. On présente ici un algorithme basé sur deux parcours en profondeur. Etant donné qu'on aura besoin de calculer le transposé d'un graphe, quelle est la structure de donnée appropriée?

Ecrire l'algorithme de parcours en profondeur pour un graphe orienté G. Chaque sommet u du graphe se voit attribuer quatre nouveaux paramètres (modifier la structure de graphe en conséquence):

une couleur (blanc, gris ou noir) selon l'état du sommet (non-visité, en cours de traitement et traité)
un parent p[u] qui permet de construire une arborescence sur les sommets
tableau de fin de traitement f[u]

Algorithme Parc_Prof(G)

pour chaque sommet u faire
  couleur[u] := blanc
  p[u] := -1
pour chaque sommet u faire
  si couleur[u]=blanc alors Visiter_PP(u)

Algorithme Visiter_PP(u)

couleur[u] := gris
pour chaque sommet v adjacent à u faire
  si couleur[v]=blanc alors
    p[v] := u
    Visiter_PP(v)
couleur[u] := noir
ajouter u au premier emplacement libre de f

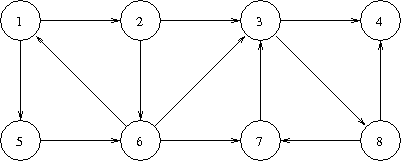
Le tester sur l'exemple :

Ecrire l'algorithme de calcul de composantes fortement connexes :

appeler Parc_Prof(G) pour calculer les dates de fin de traitement de chaque sommet
calculer le graphe transposé de G
appeler Parc_Prof(trans(G)) en traitant les sommets de f par index décroissant
renvoyer l'arborescence obtenue (chaque arbre est une composante fortement connexe de G)

Quelle est sa complexité ? Le tester sur l'exemple précédent.

On ajoute une arête à un graphe orienté. Quelles conséquences sur le nombre de composantes fortement connexes ? Montrer qu'un graphe et son graphe transposé ont les mêmes composantes fortement connexes.