:: Enseignements :: ESIPE :: E4INFO :: 2008-2009 :: Algorithmique ::
On considère les graphes orientés sans cycle, ou dags (pour directed acyclic graphs). On choisira l'implémentation par listes chaînées.
![[LOGO]](http://igm.univ-mlv.fr/ens/resources/mlv.png) | Graphes orientés sans cycles |
On considère les graphes orientés sans cycle, ou dags (pour directed acyclic graphs). On choisira l'implémentation par listes chaînées.
Exercice 1 - Détection
Ecrire une fonction qui vérifie que le graphe est un dag.
Exercice 2 - Tri topologique
Les dags peuvent représenter des étapes d'un processus (plus ou
moins) complexe : un arc entre x et y veut dire "x doit être fait
avant y". Par exemple, pour m'habiller le matin, je mets
Avec un tel graphe, on peut déterminer un ordre (non unique) dans lequel exécuter des actions : c'est le tri topologique. Ecrire une fonction qui renvoie un tableau donnant un ordre topologique.
- mon pantalon avant ma ceinture,
- ma chaussette droite avant la chaussure droite, idem pour la gauche,
- ma chemise avant ma ceinture,
- mon caleçon avant mon pantalon,
- mon pantalon avant chaque chaussure,
- ma chemise avant ma cravate,
- ma cravate avant mon pull,
- mon pull avant mon chapeau,
- ma montre n'importe quand.
Avec un tel graphe, on peut déterminer un ordre (non unique) dans lequel exécuter des actions : c'est le tri topologique. Ecrire une fonction qui renvoie un tableau donnant un ordre topologique.
Exercice 3 - Nombre de chemins
On veut une fonction qui donne le nombre de chemins entre deux
sommets s et t d'un dag.
Faire un tri topologique. Parcourir le tableau résultat, à partir de s, en propageant le nombre de chemins. Essayer sur le graphe suivant.
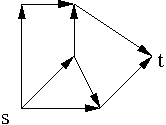
Faire un tri topologique. Parcourir le tableau résultat, à partir de s, en propageant le nombre de chemins. Essayer sur le graphe suivant.

© Université de Marne-la-Vallée