:: Enseignements :: ESIPE :: E4INFO :: 2008-2009 :: Algorithmique ::

Algorithme de Dijkstra

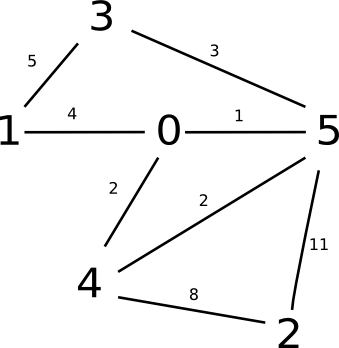
L'algorithme de Dijkstra (d'après le Danois Edsger Dijkstra) permet de calculer le plus court chemin d'un graphe non-orienté, dans le cas où tous les poids sont positifs ou nuls (sinon, il faut prendre l'algorithme de Ford-Bellman).

L'algorithme de Dijkstra est assez simple. On part du sommet source et on propage les distances. A chaque itération, on choisit le sommet ayant la plus petite distance à la source, puis on calcule les distances de ses voisins qui n'ont pas encore été visités, et on met à jour si besoin.

On aura donc besoin :

d'un tableau visite pour noter les sommets déjà visités,
d'un tableau distance pour noter la distance à la source,
d'un tableau parent pour noter d'où on vient, et reconstituer le chemin le plus court à la fin.

L'algorithme proprement dit :

dijkstra(source, destination)

pour tout sommet s
  parent[s] = inconnu
  visite[s] = non
  distance[s] = infini
distance[source] := 0

tant qu'il reste des sommets non visités
  trouver le sommet s non visité minimisant la distance
  visite[s] = oui
  pour tout sommet t adjacent à s
    si t n'a pas été visité
      si distance[t] > distance[s] + poids(arête de s à t)
        mettre à jour distance[t]
        parent[t] = s

écrire le chemin à partir de parent
renvoyer distance[destination]

Ceux qui trouve le tp trop facile constateront que la fonction qui trouve le sommet minisant la distance est a priori de complexité n. Comment peut-on l'améliorer?