:: Enseignements :: Licence :: L3 :: 2006-2007 :: Architecture des ordinateurs ::
Dans cette séance de travaux dirigés, nous allons étudier le calcul des formules logiques (algèbre de Boole). En particulier, nous allons voir les différentes représentations d'une expression logique (circuits combinatoires, expressions algébriques, tables de vérité) et comment passer de l'une à l'autre (méthodes minterms, maxterms, tables de Karnaugh).
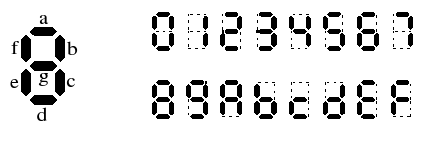
![[LOGO]](http://igm.univ-mlv.fr/ens/resources/mlv.png) | Circuits combinatoires, Algèbre de Boole, Tables de Karnaug |
Dans cette séance de travaux dirigés, nous allons étudier le calcul des formules logiques (algèbre de Boole). En particulier, nous allons voir les différentes représentations d'une expression logique (circuits combinatoires, expressions algébriques, tables de vérité) et comment passer de l'une à l'autre (méthodes minterms, maxterms, tables de Karnaugh).
Exercice 1 - Opérations logiques élémentaires
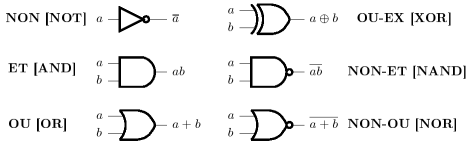
La figure suivante donne le schéma des principaux opérateurs logiques :

- Donner la table de vérité de chacun de ces opérateurs.
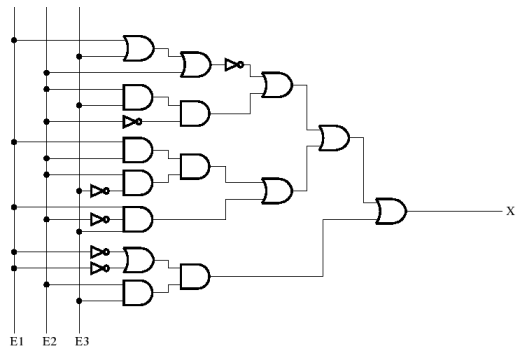
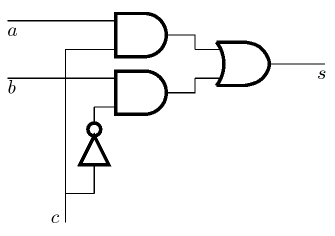
- Donner la table de vérité du circuit ci-dessous.
- Combien y a-t-il d'opérateurs logiques unaires (à une seule entrée), binaires (à deux entrées) ? Donner leurs tables de vérité et proposer des noms.
- Combien y a-t-il d'opérateurs logiques n-aires (à n entrées)?
Exercice 2 - Relations fondamentales de l'algèbre de Boole
On rappelle que $1$ désigne la constante VRAI, $0$ la constante FAUX
et que l'on note indifféremment $a\times b$ ou $ab$ le produit
logique (ET) de $a$ et $b$, la somme logique (OU) étant notée $a+b$.
- Règles des constantes:
- $\textbf{R1.} a+0=a$
- $\textbf{R2.} a\times 0=0$
- $\textbf{R3.} a+1=1$
- $\textbf{R4.} a\times 1=a$
- Idempotence (duplication)
- $\textbf{R5.} a+a=a$
- $\textbf{R6.} a\times a=a$
- Complémentation
- $\textbf{R7.} a+\overline{a}=1$
- $\textbf{R8.} a\times \overline{a}=0$
- Commutativité
- $\textbf{R9.} a+b=b+a$
- $\textbf{R10.} a\times b=b\times a$
- Distributivité
- $\textbf{R11.} a+(bc)=(a+b)(a+c)$
- $\textbf{R12.} a(b+c)=(a b)+(a c)$
- Associativité
- $\textbf{R13.} a+(b+c)=(a+b)+c=a+b+c$
- $\textbf{R14.} a(bc)=(ab)c=abc$
- Théorèmes de De Morgan
- $\textbf{R15.} \overline{ab}=\overline{a}+\overline{b}$
- $\textbf{R16.} \overline{a+b}=\overline{a}\,\overline{b}$
- Autres relations
- $\textbf{R17.} \overline{\overline{a}}=a$
- $\textbf{R18.} (a+b)(a+\overline{b})=a$
- Vérifier l'associativité ainsi que la règle de De Morgan sur les tables de vérité.
- Vérifier algébriquement les relations suivantes :
- $a+(ab)=a$
- $a+(\overline{a}b)=a+b$
- $(a+b)(a+\overline{b})=a$
- $a(a+b)=a$
Exercice 3 - Minterms-Maxterms
On appelle minterm le produit logique (ET) de plusieurs
variables ou de leurs compléments (exemple : $ab\overline{c}$). On appelle
maxterm la somme logique (OU) de plusieurs variables ou de
leurs compléments (exemple : $a+b+\overline{c}$). On veut exprimer
n'importe quelle fonction logique en utilisant seulement les
fonctions ET, OU, et NON. On va tout d'abord étudier l'exemple de la
fonction XOR.
- Dans la méthode des minterms, on utilise le fait que la fonction peut s'exprimer comme la somme logique de tous les minterms correspondant à chaque sortie $1$ dans la table de vérité. Donner l'expression du XOR par la méthode des minterms.
- Dans la méthode des maxterms, on utilise le fait que la fonction peut s'exprimer comme le produit logique de tous les maxterms correspondant à chaque sortie $0$ dans la table de vérité. Donner l'expression du XOR par la méthode des maxterms.
- Calculer avec les deux méthodes les expressions logiques
dont la table de vérité est
a\bc |00|01|10|11 ------------- 0| 1| 0| 1| 0 1| 0| 1| 1| 0
- Proposer une expression logique simplifiée, dessiner le circuit logique correspondant.
Exercice 4 - Opérateurs complets
On vient de montrer que l'on peut réaliser n'importe quel opérateur
logique en utilisant seulement des portes AND, OR, et NOT. En fait,
cet ensemble n'est pas minimal:
- Pourquoi ?
Nous allons montrer que l'on peut réaliser n'importe quel opérateur logique avec l'une seulement des deux fonctions suivantes: NAND (NON ET) et NOR (NON OU). - Donner les tables de vérité des opérateurs NAND et NOR.
- Montrer que l'on peut réaliser les opérateurs NOT, OR et AND en utilisant seulement des NAND. Même question avec des NOR.
- Conclure que l'on peut réaliser n'importe quel circuit.
- Application : réaliser le XOR en utilisant seulement des portes NAND puis avec seulement des NOR.
Exercice 5 - Analyse d'un circuit logique

- Quelle est l'expression booléenne de la sortie $X$ ?
- Donner l'expression simplifiée et le circuit correspondant en n'utilisant que les opérateurs à deux entrées choisis parmis OR, AND, XOR et NOT.
- Calculer la table de vérité de ce circuit.
- Quel est son rôle ?
Exercice 6 - Simplification par la méthode des tables de Karnaugh : réalisation d'un afficheur
Une table de Karnaugh est une manière particulière de présenter les
tables de vérité : au lieu d'écrire les entrées dans l'ordre usuel,
on les écrit dans l'ordre $00$, $01$, $11$, $10$ où seul un bit
change à chaque fois. Il est ainsi très facile de repérer les
simplifications possibles. On cherche à réaliser un circuit
afficheur hexadécimal pour une calculette. L'entrée est un nombre
$n$ en binaire sur $4$ bits : $b_0$, $b_1$, $b_2$, $b_3$. Les $7$
sorties sont appelées $a$, $b$, $c$, $d$, $e$, $f$, $g$. Une sortie
est à $1$ si le segment correpondant est noir.
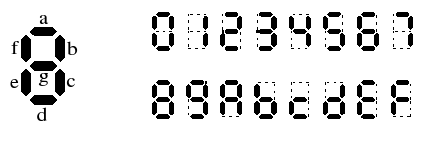
- Écrire les tables de vérité des $7$ sorties.
- En déduire le circuit correspondant.
Rappels:
n|b0|b1|b2|b3 ------------- 0| 0| 0| 0| 0 1| 0| 0| 0| 1 2| 0| 0| 1| 0 3| 0| 0| 1| 1 4| 0| 1| 0| 0 5| 0| 1| 0| 1 6| 0| 1| 1| 0 7| 0| 1| 1| 1 8| 1| 0| 0| 0 9| 1| 0| 0| 1 A| 1| 0| 1| 0 B| 1| 0| 1| 1 C| 1| 1| 0| 0 D| 1| 1| 0| 1 E| 1| 1| 1| 0 F| 1| 1| 1| 1
Exercice 7 - Tables de Karnaugh partielles
On veut maintenant réaliser un afficheur décimal. Les sorties
qui ne correspondent pas à une entrée décimale sont indéfinies. On
peut donc choisir ce qui nous arrange pour avoir le circuit le plus
simple.
- Écrire les tables de vérité partielles des $7$ sorties et les compléter pour avoir les formules les plus simples.
- En déduire le circuit correspondant.
Exercice 8 - Le code Gray
Le but de cet exercice est de trouver un moyen pour énumérer toutes
les configurations possibles des entrées d'un circuit logique de
manière à ne changer qu'une seule entrée entre deux configurations
consécutives.
- Montrer que l'on peut écrire les quatre configurations de deux entrées en ne changeant qu'une entrée à chaque fois.
- On définit alors récursivement le code Gray de la manière
suivante :
- Le code Gray d'une entrée seule est 0, 1;
- Supposons que l'on sait calculer le code Gray d'un circuit à $n$ entrées. On écrit alors les $2^n$ configurations correspondantes précédées par un $0$ puis, les $2^n$ configurations précédées par un $1$, dans l'ordre inverse.
- Écrire le code Gray sur 2, 3 et 4 entrées, vérifier que cela répond bien au problème.
© Université de Marne-la-Vallée