TP2 : Etude de files d'attente sous OMNeT++

Discrete Event Simulator - http://www.omnetpp.org/

Hakim Badis

Un rapport doit être rendu au plus tard 10 jours après le dernier TP à l’adresse e-mail suivante : badis@u-pem.fr. Le compte rendu doit contenir : un rapport pour chaque TP + les sources de chaque exercice. L’objet de l’e-mail doit respecter le format suivant : [TP-MDR][votre-formation].nom1-nom2.

I. L'affinement des mesures par la modification des graines des séquences pseudo-aléatoires générées

Les résultats obtenus précédemment sont basés sur la même graine (seed en anglais : un nombre employé pour produire une suite pseudo-aléatoire). Si on lance une nouvelle fois la simulation, nous obtiendrons exactement les mêmes résultats. En conséquence, les résultats dépendent fortement de la valeur de la graine utilisée. Affiner un résultat consiste à calculer la moyenne de plusieurs résultats où chacun utilise une graine différente.

Q1. Dans la simulation précédente (m/m/1), quelle est la valeur par défaut de la graine ?

Q2. Quel est le générateur des séquences pseudo-aléatoires utilisé ?

Pour lancer plusieurs répétitions d’une simulation avec des graines différentes, il suffit de positionner l’option Repeat count dans le fichier .ini.

Q3. Tester la configuration (1/lambda = 20s et 1/mu =12s) avec 50 répétitions. Les résultats ont-ils convergé vers ceux obtenus théoriquement ?

II. La file M/M/1/K

Avec K = 201, une répétition, et en utilisant les mêmes paramètres de l’exercice m/m/1 :

Q1. Quelles sont les valeurs moyennes pratiques et théoriques de : nombre de jobs dans la file fifo, temps d’attente dans la file fifo, temps de séjours, Taux d’occupation, nombre de jobs droppés ?

Q2. Comparer les résultats pratiques et théoriques

III. La file M/M/2

La topologie à réaliser est la suivante :

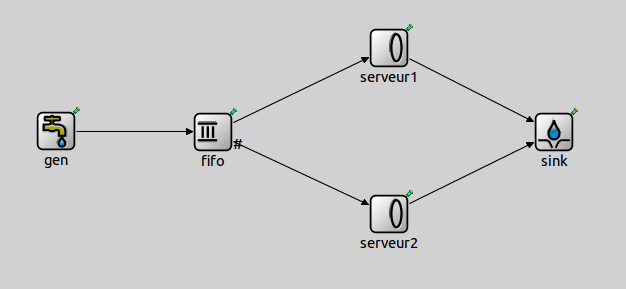
Le modèle contient 5 modules :

1. Le module gen génère des Jobs et il les envoie instantanément au module fifo. Le temps qui sépare deux générations suit une loi exponentielle de paramètre λ jobs/s.

2. Deux modules serveurs (serveur1 et serveur2). Le temps de service de chaque serveur suit une loi exponentielle de paramètre μ jobs/s.

3. Les Jobs reçus par le module fifo sont stockés dans la file d’attente si les deux serveurs sont occupés. Si l’un des serveurs est disponible, le premier client en attente choisit ce serveur.

4. Après être traités par l’un des serveurs, les jobs sont envoyés au module sink pour être détruits.

Les paramètres de la simulation sont résumés dans la table suivante

Paramètre	Valeur
1/λ	4s, 8s, 12s, 16s, 20s
1/μ	12s
Capacité de la file d’attente	∞ (capacité par défaut sous OMNeT++)
Nombre de serveurs	2
Type de la file d’attente	FIFO
Durée de la simulation	200000s
Nombre de jobs	∞ (valeur par défaut sous OMNeT++)
Nombre de répétitions par configuration	10

Q1. Quelles sont les valeurs moyennes pratiques et théoriques de : nombre de jobs dans la file, temps d’attente dans la file fifo, temps de séjours, Taux d’occupation, nombre de jobs droppés ?

Q2. Comment améliorer les résultats de la simulation pour converger le plus possible vers les résultats théoriques ?

Q3. Tracer et commenter le nombre de jobs moyen dans la file fifo (queueLenth) ainsi que le temps de séjour (lifeTime) moyen d’un job en fonction du temps de l’ensemble des configurations.

IV. Parc de serveurs

Une entreprise fournissant des services web désire renouveler son parc de serveurs informatiques. Elle a le choix entre trois options illustrées sur la figure suivante

Dans chacune des options envisagées, les files d’attente sont de capacités infinies et sont gérées suivant la discipline FIFO. On suppose que les requêtes arrivent suivant un processus de Poisson de taux λ. Une fois prise en charge par un serveur, la durée de traitement d’une requête est aléatoire et suit une distribution exponentielle de moyenne 2µ dans l’option 1, et de moyenne µ dans les options B et C.

Q1. Déterminer et prouver par simulation, la configuration qui permet de minimiser le temps de réponse moyen aux requêtes.