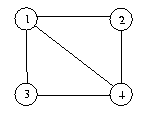
Le graphe G1
Langage de programmation : C++, Java.
Environnement de développement : au choix
Cotation de difficulté : normal à difficile
Type de sujet : algorithmique sur les graphes
Une coloration d'un graphe est une affectation de couleurs à ses sommets de façon que deux sommets joints par une arête soient affectés de couleurs différentes. Trouver le nombre minimum de couleurs nécessaires pour colorier un graphe G donné (c'est déterminer le nombre chromatique de G) est une question qui intervient dans l'établissement d'emplois du temps ou dans la gestion de ressources partagées, ou en compilation dans l'utilisation efficace de registres. C'est aussi une question qui a intrigué de nombreux mathématiciens avec le problème des quatre couleurs, celui-ci étant équivalent à démontrer que tout graphe dessiné dans le plan sans que ses arêtes se coupent a un nombre chromatique inférieur ou égal à 4. Une généralisation du nombre chromatique est la notion de polynôme chromatique associé à un graphe G, c'est un polynôme tel que pour tout entier k, P(G,k) est le nombre de façons de colorier G en k couleurs, ainsi le nombre chromatique de G est le plus petit entier k tel que P(G,k) est non nul. Ce projet vous propose de calculer des polynômes chromatiques de graphes ayant un faible nombre de sommets.

Tout graphe considéré ici est un graphe symétrique,
il est constitué d'un ensemble X de sommets et d'un ensemble
E d'arêtes, chaque arête est une paire {x,y} de sommets.
Une k-coloration d'un graphe G est une application g de X
dans l'ensemble {1,2, ..., k} telle que pour toute arête {x,y}
on ait g(x) est différent de g(y), le plus petit entier k pour lequel il existe une k coloration de G est appelé nombre chromatique de G.
On peut montrer que le nombre de k-colorations différentes de G
s'exprime sous la forme d'un polynôme en k, noté ici P(G,k). Par exemple pour une k-coloration g du graphe G1
dessiné ci-dessus, il y a k choix possibles pour g(1), k-1
pour g(3) (qui doit être différent de g(1)) et k-2 possibilités
pour g(2) et g(4) (qui doivent être différents des deux valeurs
précédentes); ainsi :
Le calcul du polynôme chromatique d'un graphe utilise deux opérations sur les graphes : la suppression et la contraction d'une arête. Soit un graphe G=(X,E) et soit e dans E une arête de G, le graphe G-e obtenu à partir de G par suppression de e a pour ensemble de sommets X et pour ensemble d'arêtes E - e. Le graphe Ge obtenu par contraction de l'arête e={x,y} a pour ensemble de sommets X - y et pour ensemble d'arêtes l'ensemble obtenu à partir de E en remplaçant chaque arête {y,z} (qui contenait y) par l'arête {x,z}, si elle n'était pas déjà dans E.
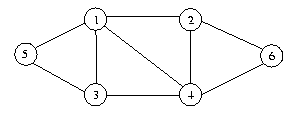
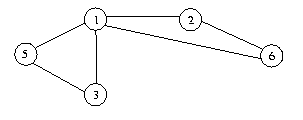
Par exemple le graphe G2 donne le graphe G'2 par
contraction de l'arête {1,4}.
On démontre assez facilement le résultat suivant :
Cette relation permet d'obtenir le polynôme chromatique des graphes ayant peu de sommets en procédant récursivement. On peut utiliser pour raccourcir les calculs, le fait que le polynôme chromatique d'un graphe sans cycle ayant n sommets est k(k-1)(n-1). On note aussi que le graphe complet ayant n sommets et toutes les n(n-1)/2 paires de sommets comme arêtes a pour polynôme chromatique k(k-1)... (k-n+1). Enfin il est assez facile de voir que le polynôme chromatique d'un graphe ayant deux composantes connexes est égal au produit des deux polynômes chromatiques de celles-ci.
Par exemple en appliquant ces techniques on trouve :
On écrira un programme qui calcule le polynôme chromatique d'un graphe ayant environ une quinzaine de sommets. Il devra être représenté en mémoire par des listes chaînées de voisins. On tachera de limiter la profondeur des appels récursifs en reconnaissant des graphes pour lesquels le polynôme chromatique est connu.
Une partie interface graphique est demandée pour pouvoir saisir graphiquement un petit graphe.
On lira les pages d'informations générales sur le travail demandé.