Un test pour les codes, et applications
Introduction
Un procédé simple de codage consiste à substituer, à chaque
caractère du texte source, une
chaîne de caractères sur un autre alphabet, et de transmettre la
séquence substituée.
L'exemple le plus répandu est le code Morse, où l'alphabet de
codage est composé de trois
éléments (point, trait, blanc). Le codage de Huffman, utilisé en
compression de données, est
un autre exemple, sur un alphabet binaire cette fois.
Dans tous les cas, l'on demande bien évidemment que le codage soit
réversible, c'est-à-dire
que le message codé soit déchiffrable sans ambiguïté, en
d'autres termes que l'application
de codage soit injective.
Dans les deux exemples (Morse et Huffman),
le décodage est instantané, c'est-à-dire que le décodage peut se faire
dès que la fin d'un mot du code est reconnue. Ceci est loin d'être le
cas général.
Le présent projet est centré autour des codes, et du délai de
déchiffrage. Il comporte la programmation
programmation d'un algorithme
qui teste si un ensemble fini de mots est un code,
et dans l'affirmative, du calcul du délai de déchiffrage,
et si ce délai est fini, d'une fonction de décodage.
Si l'ensemble testé n'est pas un code, on calcule le
plus petit code (dans un sens à préciser) qui permet d'émettre les
messages sans ambiguïté.
1 Définitions
Soit A un ensemble fini, appelé alphabet. Ses éléments sont appelés lettres.
Un mot est une suite finie,
éventuellement vide, de lettres. La longueur d'un mot w est le nombre de
lettres qui le composent. Elle est notée |w|. Le seul mot de longueur 0 est le
mot vide noté e. L'ensemble des mots sur A, est muni d'une loi de composition appelée
concaténation ou produit, et qui à deux mots u et v associe
le mot uv obtenu en mettant bout à bout
u et v. Un mot x est préfixe de w s'il existe y tel que w=xy.
C'est un préfixe propre non vide si x n'est pas le mot vide
et x¹ w. Même définition pour les suffixes. Un mot
x est facteur de w s'il existe y,z tel que w=yxz.
On note A* l'ensemble des mots sur A.
Exemple. Si A={a,b,c}, le produit des
mots u=ac et v=bac est uv=acbac. Ce mot a les
facteurs e, a, b, c, ac, ba, cb, acb, cba, bac, acba, cbac et acbac. Ses préfixes sont
e, a, ac, acb, acba et acbac. Les mots e et ac sont à la fois préfixes et suffixes.
Un ensemble fini X de mots de A* est un code si, pour tous x1,... ,xn, y1,... ,ym
dans X, l'équation
x1··· xn=y1··· ym
implique m=n et xi=yi pour i=1,... ,n.
Exemple. L'ensemble X={a,bb,abbba,babab} n'est pas un code parce que
a· bb· babab· abbba = abbba· babab· bb· a
En revanche, l'ensemble X= {a, ab, bb} est un code, car si x1··· xn=y1··· ym, on a
xn=ym parce qu'un mot ne peut pas se terminer à la fois par ab et par bb.
2 Algorithme de Sardinas et Patterson
Cet algorithme permet de tester si un ensemble fini X de mots est un code. Pour ce faire, on
construit un graphe G(X)=(P,U), où P est l'ensemble des préfixes non vides de mots de X,
et U l'ensemble des couples (u,v) tels que
-
uvÎ X ou
- vÏ X et il existe xÎ X tel que ux=v.
Un arc croisé est un arc de la première espèce, un arc avant un arc du deuxième
type.
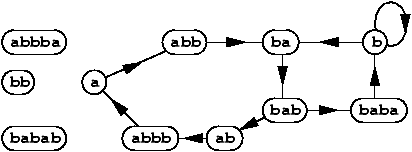
Figure 1.--- Le graphe G(X) pour X={a,bb,abbba,babab}.
Exemple. Pour X={a,bb,abbba,babab}, l'ensemble P contient, en plus de X, les mots
{b, ab, abb, abbb, b, ba, bab, baba}.
Les arcs avant sont (a,abb), (ab, abbb), (b, ba), (bab, baba).
Les arcs croisés sont (b,b), (abb,ab), (abbb,a), (ba,bab), (bab, ab), (baba, b).
Le graphe G(X) est donné dans la figure 1.
On montre qu'un ensemble X est un code si et seulement s'il n'y a
pas de chemin, dans G(X), qui relie un sommet appartenant à X à un sommet appartenant à X.
En effet, un tel chemin décrit une double factorisation. Dans notre exemple, le circuit autour du
sommet a correspond à la double factorisation donnée plus haut.
Travail 1.
Implémenter l'algorithme de manière efficace. Il devra
construire le graphe d'un
ensemble de mots, l'afficher de
manière textuelle ou graphique, et dire si l'ensemble donné est un
code ou non. Dans la négative, il donnera une ``preuve'' en affichant
un
mot qui possède une double décomposition.
3 Délai de déchiffrage
Pour un code X, décoder un message revient à trouver sa décomposition en mots du
code. En procédant de gauche à droite dans la lecture du message, on
repère les mots du code dans le début du message, et on les retient
dès que l'on est sûr qu'ils correspondent la décomposition finale.
Exemple. 1.-- L'ensemble X={a,ba,bb} est
un code. La décomposition d'un message est déterminée dès la lecture
d'un mot du code, car aucun mot du code n'est préfixe d'un autre (code
dit préfixe.
2.-- L'ensemble X={ab,ababa,baa} est aussi un code. Ici, la
connaissance du début abababa ne permet pas encore de savoir si la
décomposition commence par ab· ab· ab· a ou par
ababa· ba. Ce n'est qu'après la lecture de la lettre
suivante que l'on sait si la décomposition commence par ab (si
la lettre est b) ou par ababa.
Un code X est a délai de déchiffrage fini s'il existe
un entier d tel que, chaque fois qu'un message w commence par
p=x1x2··· xd+1 (avec x1,...,d+1Î X),
alors la factorisation complète de w commence par x1.
C'est donc après un ``délai'' de d mots de code que l'on
peut affirmer que le premier mot trouvé est le bon.
Si un code est à délai de déchiffrage fini, le plus petit entier d
admissible est le délai de déchiffrage.
Exemple. Le code X={a,ba,bb} a délai
0. Le code X={ab,ababa,baa} a délai 2. Le code X={aa, ba,
b}
a délai infini car pour tout d, le mot b(aa)d est préfixe de
ba(aa)d, et on ne peut décider si la factorisation commence par b
ou ba.
On montre que le délai est infini si et
seulement si G(X) a un circuit.
Si G(X) est sans circuit, chaque chemin c issu d'un sommet dans
X reçoit un poids p(c). Pour cela, on lui associe le nombre
d(c) (=0 ou 1) récursivement par: d(c) = 1 si c
est un arc, et d(ce)=d(c) si e est un arc avant, et d(ce) =
1-d(c) si e est un arc croisé.
Ensuite, on définit deux valeurs h(c) et b(c)
récursivement par:
h(c)=1, b(c)=0 si c est arc, et
h(ce)=d(ce)+h(c) et b(ce)= 1-d(ce)+b(c).
Le poids p(c) d'un chemin c est le maximum des nombres h(c) et
b(c).
On montre que d+1 est le maximum des poids des chemins issus de
sommets dans X.
Exemple. Considérons le chemin
(a,x,x,x,a), où on a écrit a pour un arc avant, et x pour un arc
croisé. La fonction d prend les valeurs (1,0,0,0,1),
la fonction h vaut (1,1,1,1,2) et b vaut (0,1,2,3,3).
Le poids de ce chemin est 3.
Travail 2. Implémenter l'algorithme qui
teste si un code X a délai de déchiffrage fini. Dans l'affirmatve,
calculer le délai de déchiffrage et donner un mot que est une
``preuve''
que le délai est atteint.
Travail 3. Implémenter un algorithme de décodage
pour un code dont on sait qu'il a délai de déchiffrage d.
4 Enveloppe libre
Pour tout ensemble X de mots, on note X* l'ensemble des mots
qui sont produits de mots de X, soit X*={x1··· xn|
n³0, x1,..., xnÎ X}.
L'enveloppe libre d'un ensemble X est le code Y tel que
X*Ì Y* et Y* minimal. Cela signifie que tout élément de
X est produit d'éléments de Y, et que Y est choisi tel que
l'ensemble
des mots supplémentaires (dans Y* sans être dans X*) est le plus
petit
possible. Si X est un code, il est égal à son enveloppe libre.
On montre que l'enveloppe libre existe toujours et, si X n'est pas un
code, a
strictement moins d'éléments que X.
Exemple. L'ensemble
X={aa,bb,aabbbaa,baabaab} n'est pas un code.
Son enveloppe libre est {aa,b}.
Pour calculer l'enveloppe libre Y de X , on procède comme suit.
On calcule G(X) pour tester si X est un code. Si c'est le cas,
Y=X.
Sinon, on détermine l'ensemble C(X) des mots qui figurent sur les
chemins reliant des mots de X et qui sont des sommets d'arrivée
d'arcs croisés de ces chemins.
On supprime, dans X'=XÈ C(X) les mots
qui sont produits d'autres mots de X'. Soit X'' l'ensemble obtenus.
On recommence avec X''. Comme les mots de X'' sont plus courts que
ceux de X, le procédé s'arrête. On peut montrer que X'' a la même
enveloppe libre que X. Le dernier ensemble obtenu est donc Y.
Exemple. Pour l'ensemble
X={aa,bb,aabbbaa,baabaab},
l'ensemble C(X) est {aa, baa, baab, aab, b}. L'ensemble
X'' est {aa,b} parce que tout mot de X est produit de mots de
X''.
Exemple. Pour X= {a, ab, ba, abbc,
bcca, caab}, on a C(X)={ab, bc, ca, b, a}, d'où
X''={a, b, bc, ca}. L'ensemble X'' n'est pas un code, et en
recommençant,
on trouve Y={a,b,c}.
Travail 4. Implémenter l'algorithme qui
calcule l'enveloppe libre d'un ensemble fini de mots.
5 Ce qui est demandé
Le but du projet est la réalisation des 4 tâches décrites ci-dessus,
dans l'ordre. Il est important de décrire, dans le rapport, les
algorithmes
et les structures de données choisies. Cette description doit être
précise et justifiée: si l'on utilise un tableau plutôt qu'une liste
ou vice-versa, il y a certainement des raisons. Utiliser au mieux les
fonctions de la classe String.
Pour tester vos programmes, voici quelques exemples non exhaustifs. Pour chacun,
vous pouvez déterminer si c'est un code, quel est son délai, et si ce n'est pas un
code,
calculer l'enveloppe libre.
(1) X={a,ab,bb}
(2) X={a,ba,bb}
(3) X={b,ab,abb,abaa,aaaa}
(4) X={b,ab,aab,abba}
(5) X={ab,baab,abb} et X={ab,baab,abb, bbab}
(6) X={aa,ba,bb,baa,bba}
(7) X={ab,ababa,baa}
(8) X={a, ab, ba, abbc, caab, bcca}
(9) X={a, ab, ba, abbc, caab, bcca, abbcabbd, bccdbcca, cddacddb,
daabdaac} etc.
This document was translated from LATEX by
HEVEA.