


Next: Arrays
Up: Automaton Representations
Previous: Single vector (compact representation)
It consists in implementing a list of triples in 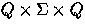 using a hash table mapping couples of
using a hash table mapping couples of  on P(Q). This is a
good trade-off between speed and memory : transition access is performed in
almost constant time (depending on the quality of the hashing function) and
memory use is proportional to the number of transitions. It is recommended
anyway to have an idea of the number of transitions beforehand to avoid
reallocation during computation (see table
5).
on P(Q). This is a
good trade-off between speed and memory : transition access is performed in
almost constant time (depending on the quality of the hashing function) and
memory use is proportional to the number of transitions. It is recommended
anyway to have an idea of the number of transitions beforehand to avoid
reallocation during computation (see table
5).
Vincent Lemaout
12/9/1997