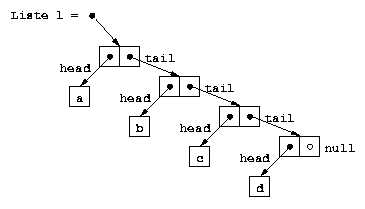
Une liste est constituée:

Une telle structure peut être implantée par la classe suivante. Notons simplement ici que, par polymorphisme, on peut déclarer le type des éléments de la liste comme des Object, afin que la liste puisse stocker n'importe quel type d'objet (comme ici, des String). Dans le cas ou on désire stocker des types primitifs (comme des int), on peut alors soit passer par leur type enveloppe (Integer), soit définir le champ head directement du type primitif voulu (int); dans ce dernier cas, la liste n'est alors plus générique, mais dédiée à un type unique.
/**
* Une classe implantant le type récursif des listes.
*/
public class Liste {
Object head;
Liste tail;
/**
* Constructeur (seule façon de créer une liste non vide).
*/
public Liste(Object head, Liste tail) {
this.head = head;
this.tail = tail;
}
/**
* Longueur de la liste.
*/
public int length() {
if (tail == null)
return 1;
return 1 + tail.length();
}
/**
* Représentation d'une liste.
*/
public String toString() {
if (tail == null)
return "[" + head + ":" + "[]" + "]";
return "[" + head + ":" + tail.toString() + "]";
}
/**
* Teste si la liste contient un élément donné.
*/
public boolean contains(Object o) {
if (head.equals(o))
return true;
if (tail == null)
return false;
return tail.contains(o);
}
public static void main(String[] args) {
Liste l = new Liste("a",
new Liste("b",
new Liste("c",
new Liste("d",null))));
System.out.println(l);
System.out.println("longueur: " + l.length());
System.out.println("Contient c? " + l.contains("c"));
}
}
Le premier problème que pose cette implémentation des listes est le
suivant: comment faire pour connaître la longueur d'une liste qui est
vide, telle que
Liste listeVide = null;
Exercice 1: Trouver une solution permettant de résoudre ce problème. Pensez à faire en sorte qu'il n'existe qu'une seule instance de la liste vide.
Dans le programme résultant, comme dans beaucoup d'algorithmes sur des structures récursives, on décrit les algorithmes selon le cas dans lequel on se trouve: soit sur un maillon normal (c'est le cas récursif), soit sur le maillon terminal (la liste vide est le cas de terminaison de la récursion).
Dans les langages orientés objets, il est possible de décrire de manière très simple les algorithmes récursifs sur les structures récursives à condition d'avoir associé à chaque type de maillon un type de donné distinct, chacun de ces types de maillons étant un sous-type du type général. Ici, on va construire deux sous-types du type des listes: le type Cons pour les maillons qui possèdent un élément et une sous-liste et le type Nil pour les maillons terminaux, i.e., la liste vide.
Exercice 2: À partir de l'interface IList donnée ci-dessous, créez la classe Cons qui l'implante, et qui représente les maillons stockant un élément, ainsi que la classe NIL, qui implante éalement l'interface IList et qui représente les listes vides. On prendra soin de définir des méthodes toString() permettant d'obtenir une représentation sous la forme d'une chaîne de caractères des listes.
public interface IList {
/**
* Retourne la longueur de la liste.
*/
int length();
/**
* Teste si la liste contient l'objet o parmi ses éléments.
*/
boolean contains(Object o);
}
La concaténation l3 purement applicative de la liste l1 avec la liste l2 est la mise "bout à bout" des deux listes de sorte à ce que cette opération laisse inchangée les listes l1 et l2. Voici par exemple la concaténation effectuée pa la méthode append que l'on souhaite développer:
IList l1 = new Cons("a", new Cons("b", new Nil()));
IList l2 = new Cons("c", new Cons("d", new Nil()));
IList l3 = l1.append(l2);
System.out.println(l1); // [a,[b,[]]]
System.out.println(l2); // [c,[d,[]]]
System.out.println(l3); // [a,[b,[c,[d,[]]]]]
Exercice 3: Modifiez l'interface IList de sorte à ce qu'elle déclare cette méthode append, puis implantez cette méthode dans les classes Cons et Nil.
Les arbres, en informatique, on les racines en haut et les feuilles en bas:-) Ils représentent, à l'instar des listes, une structure récursive par excellence. En effet, un arbre binaire qui possède des valeurs à chacun de ses noeuds est constitué de deux sous-types: d'une part les noeuds qui stockent une valeur et deux sous-arbres (gauche et droit) et d'autre part les noeuds vides (quelque fois appelés feuilles, ou "bouts") qui sont simplement des arbres vides.
Exercice 4: Définissez l'interface Tree de ces arbres binaires, avec les déclarations des méthodes: size() qui retourne le nombre de valeurs stockées dans l'arbre, depth() qui retourne la profondeur de l'arbre (la longueur de la branche la plus longue de la racine à une feuille), contains(Object o) qui retourne vrai si la valeur o est stockée dans l'arbre et faux sinon.
Exercice 5: Définissez deux classes implémentant l'interface Tree: une classe Empty représentant l'arbre vide et une classe Node représentant un noeud, dans lequel sera stocké une valeur et les accès aux sous-arbres gauche et droit de ce noeud.
Exercice 6: Redéfinissez, dans un premier temps, la méthode toString() de sorte à pouvoir afficher une représentation de ces arbres sous la forme d'une chaîne de caractères. Comme cette représentation n'est pas très visuelle, imaginez une méthode permettant, étant donné un arbre t créé par les instructions suivantes:
Tree t = new Node("a",
new Node("b",
new Node("c",Empty.E,Empty.E),
new Node("d",Empty.E,Empty.E)),
new Node("e",
Empty.E,
new Node("f",
new Node("g",Empty.E,Empty.E),
Empty.E)));
de l'afficher sous la forme suivante:
------f ---------g ---e a ------d ---b ------c
Programmez les exercices de cette feuille et envoyez-les moi par mail.