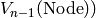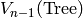Algorithmes¶
On demande d’implanter les algorithmes de calculs suivants (dans ce qui suit rule est une règle quelconque):
Calcul de la valuation d’une grammaire (ce qui permet de vérifier la grammaire);
méthode rule.count_naive(self, n) qui calcule le nombre d’objets d’un poids donné n par la méthode naïve;
méthode rule.count(self, n) qui calcule le nombre d’objets de poids n par la méthode des séries génératrices;
méthode rule.list(self, n) qui calcule la liste des objets de poids n;
méthode rule.unrank(self, n) qui calcule le i-ème élément de la liste des objets de poids n, sans calculer la liste;
Attention
Note importante: en Sage la position dans une liste commence à 0;
méthode rule.random(self, n) qui choisit équitablement au hasard un objet de poids n (on utilisera rule.unrank(self, n, i) où i sera choisi aléatoirement).
Le calcul de la valuation est nécessaire aux étapes suivantes qui sont indépendantes. Je les ai néanmoins classé par ordre croissant de difficulté.
Calcul de la valuation¶
La valuation du non-terminal nt est la taille du plus petit objet qui en dérive. La valuation d’une grammaire est l’ensemble des valuations des terminaux. Elle vérifie les quatres règles suivantes:
- la valuation d’un Singleton est 1;
- la valuation d’un Epsilon est 0;
- la valuation de l’union Union des non-terminaux
 et
et  est le
minimum des valuations de
est le
minimum des valuations de  et de
et de  ;
; - la valuation du produit Prod des non-terminaux
 et
et  est la
somme des valuations de
est la
somme des valuations de  et de
et de  ;
;
Pour la calculer, on utilise l’algorithme de point fixe suivant. On part de la
valuation 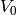 (incorrecte) qui associe à chaque non-terminal la valeur
(incorrecte) qui associe à chaque non-terminal la valeur
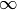 . En appliquant une fois non récursivement (pour éviter les boucles
infinies) les règles précédentes à partir de
. En appliquant une fois non récursivement (pour éviter les boucles
infinies) les règles précédentes à partir de 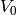 , on calcule une nouvelle
valuation
, on calcule une nouvelle
valuation 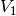 . On calcule ensuite de même une valuation
. On calcule ensuite de même une valuation  a partir de
a partir de
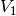 . On recommence tant que la valuation
. On recommence tant que la valuation 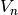 est différente de
est différente de
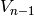 . La valuation cherchée
. La valuation cherchée  est obtenue quand
est obtenue quand 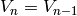 .
.
Note
Si  pour un certain non terminal
pour un certain non terminal 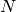 , alors
aucun objet ne dérive de ce non-terminal. On considère alors que la
grammaire est incorrecte.
, alors
aucun objet ne dérive de ce non-terminal. On considère alors que la
grammaire est incorrecte.
Par exemple, sur les arbres, le calcul se fait en  étapes:
étapes:
n: Tree Leaf Node Règle: 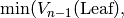

0 1 2 3 4 Final:
À faire:¶
- Écrire un fonction init_grammar qui prend en paramètre une grammaire, qui appelle sur chaque règle de la grammaire la méthode set_grammar et qui implante l’algorithme de calcul de la valuation.
Comptage naïf du nombre d’objets¶
Le comptage du nombre d’objets de poids 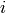 se fait en appliquant
récursivement les règles suivantes:
Soit
se fait en appliquant
récursivement les règles suivantes:
Soit 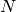 un non-terminal. On note
un non-terminal. On note 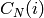 le nombre d’objet de poids
le nombre d’objet de poids 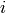 .
.
si
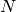 est un Singleton alors
est un Singleton alors  et
et  si
si 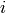 est
différent de
est
différent de  ;
;si
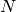 est un Epsilon alors alors
est un Epsilon alors alors 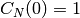 et
et 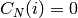 si
si 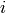 est différent de
est différent de  ;
;si
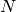 est l’union Union des non-terminaux
est l’union Union des non-terminaux  et
et  alors
alors
si
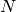 est le produit Prod des non-terminaux
est le produit Prod des non-terminaux  et
et 

Note
Pour aller plus vite et éviter des boucles infinies, on ne considérera dans la somme précédente que les cas où
 et
et 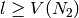 , où
, où 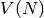 désigne la valuation du
non-terminal
désigne la valuation du
non-terminal 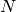 . En effet, par définition
. En effet, par définition 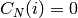 si
si  .
.
À faire:¶
- Implanter pour chaque règle de grammaire une méthode count_naive qui compte le nombre d’objets d’une grammaire dérivant d’un non-terminal et d’un poids donné.
Calcul de la liste des objets¶
On applique récursivement les définitions des constructeurs
Singleton, Epsilon, Union et Prod pour
construire la liste des objets de taille 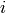 . En particulier, si
. En particulier, si 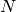 est le
produit Prod des non-terminaux
est le
produit Prod des non-terminaux  et
et  , la liste des objets
dérivant de
, la liste des objets
dérivant de 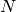 et de poids
et de poids 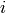 est la concaténation des listes de tous les
produits cartésiens d’éléments dérivant de
est la concaténation des listes de tous les
produits cartésiens d’éléments dérivant de  et de taille
et de taille  et
d’éléments dérivant de
et
d’éléments dérivant de  et de taille
et de taille 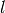 , pour tous les couples
, pour tous les couples 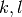 tels que
tels que 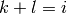 ,
, 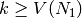 et
et 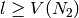 (comme précédemment
(comme précédemment
 désigne la valuation du non-terminal
désigne la valuation du non-terminal  ).
).
Par exemple, pour obtenir les arbres de taille 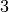 , on procède de la manière
suivante
, on procède de la manière
suivante
Calcul de Tree = Union (Leaf, Node) avec
 .
.Application de Leaf = Singleton Leaf avec
 , on retourne
la liste vide [];
, on retourne
la liste vide [];Application de Node = Prod(Tree, Tree) avec
 . La valuation
de Tree est 1. Il y a donc deux possibilités
. La valuation
de Tree est 1. Il y a donc deux possibilités 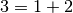 ou
ou 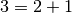 .
.- Application de Tree = Union (Leaf, Node) avec
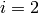 .
.- Leaf est vide avec
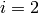 on retourne la liste vide.
on retourne la liste vide. - Application de Node = Prod(Tree, Tree) avec
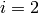 . La valuation
de Tree est 1. Une seule décomposition est possible
. La valuation
de Tree est 1. Une seule décomposition est possible 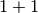 . On
appelle donc deux fois Tree avec
. On
appelle donc deux fois Tree avec 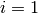 dots(Je n’écrit pas les
appels récursifs) qui retourne la liste [Leaf]. On retourne donc
la liste [Node(Leaf, Leaf)]
dots(Je n’écrit pas les
appels récursifs) qui retourne la liste [Leaf]. On retourne donc
la liste [Node(Leaf, Leaf)]
- Leaf est vide avec
- Application de Tree = Union (Leaf, Node) avec
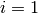 .
On retourne la liste [Leaf]
.
On retourne la liste [Leaf]
Le produit cartésien des deux listes précédentes est la liste formée du seul élément [Node(Node(Leaf, Leaf), Leaf)]
- Application de Tree = Union (Leaf, Node) avec
- Application de Tree = Union (Leaf, Node) avec
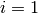 .
On retourne donc la liste [Leaf]
.
On retourne donc la liste [Leaf] - Application de Tree = Union (Leaf, Node) avec
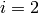 .
On retourne donc la liste [Node(Leaf, Leaf)]
.
On retourne donc la liste [Node(Leaf, Leaf)]
Le produit cartésien des deux listes précédentes est la liste formée du seul élément [Node(Leaf, Node(Leaf, Leaf))]
- Application de Tree = Union (Leaf, Node) avec
On retourne donc la liste des deux arbres:
[Node(Leaf, Node(Leaf, Leaf)), Node(Node(Leaf, Leaf), Leaf)]
Pour 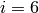 , il faut essayer les décompositions
, il faut essayer les décompositions  ,
, 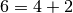 ,
, 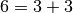 ,
,
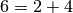 et
et 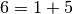 . Étudions le cas
. Étudions le cas 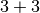 . Par appel récursif on trouve deux
arbres de poids
. Par appel récursif on trouve deux
arbres de poids 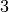 :
:
[Node(Node(Leaf, Leaf), Leaf); Node(Leaf, Node(Leaf, Leaf))]
Le produit cartésien est donc formé de  éléments qui correspondent aux
éléments qui correspondent aux  arbres suivants:
arbres suivants:
Node(Node(Leaf, Node(Leaf, Leaf)), Node(Node(Leaf, Leaf), Leaf));
Node(Node(Node(Leaf, Leaf), Leaf), Node(Node(Leaf, Leaf), Leaf));
Node(Node(Leaf, Node(Leaf, Leaf)), Node(Leaf, Node(Leaf, Leaf)));
Node(Node(Node(Leaf, Leaf), Leaf), Node(Leaf, Node(Leaf, Leaf)));
Calcul à l’aide des séries génératrices¶
En sage, chaque variable formelle doit être déclarée à l’aide de la commande var. On peut ensuite manipuler des expressions où la variable apparaît. Voici par exemple la résolution à la main du cas des arbres binaires:
sage: var("tr")
sage: sys = [tr == x + tr*tr]
sage: sol = solve(sys, tr, solution_dict=True)
sage: sol
[{tr: -1/2*sqrt(-4*x + 1) + 1/2}, {tr: 1/2*sqrt(-4*x + 1) + 1/2}]
On a alors deux solutions:
sage: s0 = sol[0][tr]
sage: s1 = sol[1][tr]
sage: taylor(s0, x, 0, 5)
14*x^5 + 5*x^4 + 2*x^3 + x^2 + x
sage: taylor(s1, x, 0, 5)
-14*x^5 - 5*x^4 - 2*x^3 - x^2 - x + 1
Pour trouver quelle est la bonne on peut remplacer 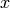 par zéro:
par zéro:
sage: s0.subs(x=0), s1.subs(x=0)
(0, 1)
Dans le cas où la série est une fraction rationnelle, on sait que le dénominateur encode la récurrence. Ceci permet un calcul beaucoup plus rapide. Pour savoir si une expression est une fraction rationnelle, il faut la factoriser, extraire le numérateur et le dénominateur et vérifier que ce sont bien des polynômes.
Note
Dans le cas des arbres binaires, cette méthode ne marche pas
sage: s0
-1/2*sqrt(-4*x + 1) + 1/2
sage: s0.factor().numerator().is_polynomial(x)
False
Voici un exemple d’une fraction rationnelle:
sage: ex = x*2/(2*x^2+x+1) + 2*x+1
sage: ex = ex.factor(); ex
(4*x^3 + 4*x^2 + 5*x + 1)/(2*x^2 + x + 1)
sage: ex.numerator().is_polynomial(x)
True
sage: ex.denominator().is_polynomial(x)
True
On peut alors extraire les coefficients:
sage: ex.denominator().coefficients(x)
[[1, 0], [1, 1], [2, 2]]
À faire:¶
- Écrire une fonction qui transforme une grammaire en un système d’équations sur des séries génératrices.
Puisque la grammaire est supposée rationnelle, le système ainsi obtenu est linéaire. La fonction solve permet de résoudre un tel système, elle fonctionne essentiellement par pivot de Gauss. La solution est alors une fraction rationnelle.
- À l’aide de la fonction précédente, ajouter une méthode generating_series aux différentes classes représentant les règles de grammaire.
La fonction taylor permet alors de calculer les premiers coefficients. Pour calculer les suivants, on utilise le fait que le dénominateur encode une récurrence vérifiée par les coefficients de la série. Ainsi, si
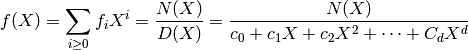
et si 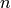 est supérieur au degré du numérateur, alors le coefficient
de
est supérieur au degré du numérateur, alors le coefficient
de 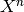 de
de 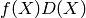 est nul. On peut sans perte de généralité
supposer
est nul. On peut sans perte de généralité
supposer 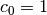 . On obtient donc les équations pour tout
. On obtient donc les équations pour tout
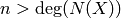 ,
,

- Écrire une méthode qui calcule les coefficients de la série en utilisant la récurrence.
Il est possible d’abaisser la complexité du calcul de 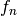 utilisant une
matrice. En effet, la récurrence s’écrit
utilisant une
matrice. En effet, la récurrence s’écrit
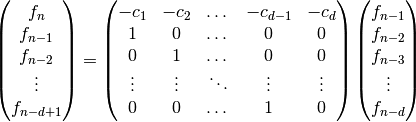
Pour calculer coefficient 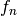 il suffit donc d’élever la matrice à la
puissance
il suffit donc d’élever la matrice à la
puissance 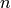 par exponentiation binaire.
par exponentiation binaire.
- Écrire une fonction qui calcule le coefficient de
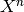 d’une fraction
rationnelle par la méthode matricielle.
d’une fraction
rationnelle par la méthode matricielle.
Calcul du 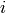 -ème élément : la méthode unrank¶
-ème élément : la méthode unrank¶
Pour calculer l’élément de taille 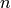 et de rang
et de rang 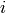 , on fait appel à la
méthode unrank. Voici par exemple l’arbre de taille
, on fait appel à la
méthode unrank. Voici par exemple l’arbre de taille 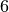 et de rang
et de rang
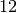 :
:
sage: treeGram['Tree'].unrank(6, 12)
Node(Leaf, Node(Node(Node(Leaf, Node(Leaf, Leaf)), Leaf), Leaf))
Attention
La numérotation commence à zéro.
On procédera récursivement comme suit:
si l’on demande un objet dont le rang est supérieur au nombre d’objet on lève une exception ValueError.
dans le cas EpsilonRule ou SingletonRule, on retourne l’objet.
dans le cas d’une union: "U" : UnionRule("A", "B"), on suppose connu les nombres d’objets:
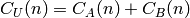 . Alors l’objet de
. Alors l’objet de  de rang
de rang
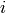 est l’objet de
est l’objet de 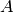 de rang
de rang 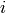 si
si 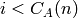 et l’objet de
et l’objet de 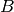 de rang
de rang
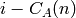 sinon.
sinon.dans le cas d’un produit: "U" : ProductRule("A", "B"), on suppose connu les nombres d’objets:
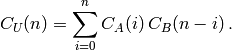
En s’inspirant de l’union, on calcule la valeur de
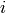 :
: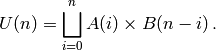
Il reste finalement à trouver l’élément de rang
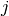 d’un produit cartésien
d’ensemble
d’un produit cartésien
d’ensemble  où
où 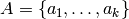 est de cardinalité
est de cardinalité  et
et
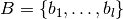 est de cardinalité
est de cardinalité 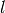 . Si l’on choisi l’ordre
lexicographique pour énumérer
. Si l’on choisi l’ordre
lexicographique pour énumérer  :
: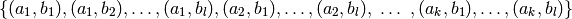
alors l’élément
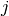 est
est 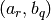 où
où  et
et  sont respectivement
le quotient et le reste de la division euclidienne de
sont respectivement
le quotient et le reste de la division euclidienne de 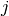 par
par  que l’on
peut calculer en sage par la méthode quo_rem des entiers.
que l’on
peut calculer en sage par la méthode quo_rem des entiers.Par exemple, pour les arbre de taille
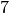 :
: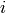
0
1
2
3
4
5
6
7
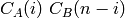
0
42
14
10
10
14
42
0
Ainsi, si l’on veut l’arbre de rang
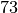 , comme
, comme 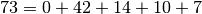 . On
prendra
. On
prendra 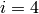 et l’on retournera l’arbre de rang
et l’on retournera l’arbre de rang  du produit cartésien
du produit cartésien
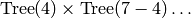 On a maintenant
On a maintenant  ,
,
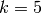 ,
,  . On retournera donc l’arbre Node(u,v) où
. On retournera donc l’arbre Node(u,v) où  est
l’arbre de taille
est
l’arbre de taille  et de rang
et de rang 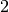 et
et  l’arbre de taille
l’arbre de taille 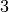 de rang
de rang
 .
.
À faire:¶
- Écrire une méthode unrank qui calcule l’élément de taille
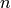 et de
rang
et de
rang 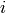 .
.