Cryptographie symétrique¶
Ce sont les systèmes, qui, comme les exemples classiques vus au premier cours, fonctionnent avec une clé secrète partagée. Il en existe principalement deux types :
les chiffrements par blocs (block ciphers):
le texte clair est divisé en blocs de $N$ caractères (en général $N$ bits), et chacun d'eux est chiffré en un bloc de $M$ caractères (en général, $M=N$);les chiffrements par flux (stream ciphers) : on superpose au texte clair une suite pseudo-aléatoire, supposée imprédictible si on ne connaît pas la clé.
Par exemple, les chiffres monoalphabétiques opèrent sur des blocs de 1 caractère, et les chiffres polyalphabétiques sur des blocs de $N$ caractères, où $N$ est la longueur de la clé.
Parmi les chiffres en usage actuellement, DES (Data Encryption Standard),
maintenant remplacé par AES (Advanced Encryption Standard, ex Rinjdael),
Blowfish,
IDEA, sont des chiffrements par blocs.
RC4 (utilisé pour le WiFi, pdf, …) A5/1
(téléphonie mobile GSM), ou le one-time pad sont des chiffrements par flux.
Avec Python, on pourra utiliser le paquetage pycrypto, ou le plus récent pycryptodome.
import Crypto
help(Crypto)
Help on package Crypto:
NAME
Crypto
PACKAGE CONTENTS
Cipher (package)
Hash (package)
IO (package)
Math (package)
Protocol (package)
PublicKey (package)
Random (package)
SelfTest (package)
Signature (package)
Util (package)
DATA
__all__ = ['Cipher', 'Hash', 'Protocol', 'PublicKey', 'Util', 'Signatu...
VERSION
3.10.4
FILE
/home/jyt/anaconda3/lib/python3.11/site-packages/Crypto/__init__.py
Le DES (Data Encryption Standard)¶
Le prototype du chiffrement par blocs est le DES (maintenant abandonné au profit de l'AES).
Adopté comme standard aux USA en 1976. C'est une modification du chiffre Lucifer d'IBM, demandée par la NSA. On a longtemps supposé que cette modification était destinée à affaiblir l'algorithme. On a depuis découvert qu'elle lui permettait de résister à des attaques qui n'ont été rendues publiques que bien plus tard.
Le standard DES a été remplacé en 2001 par l'AES (Advanced Encryption Standard).
Il est déjà suffisamment complexe pour qu'on se contente d'une étude superficielle. Avant de l'aborder, commençons par nous familiariser avec son utilisation.
Le DES transforme un bloc de 64 bits en un autre bloc de 64 bits. Il utilise des clés de 56 bits, représentées sur 64 bits (avec un bit de contrôle de parité dans chaque octet).
Il est décrit par une structure de Feistel (du nom de Horst Feistel, auteur de Lucifer).
from Crypto.Cipher import DES
help(DES)
Help on module Crypto.Cipher.DES in Crypto.Cipher:
NAME
Crypto.Cipher.DES - Module's constants for the modes of operation supported with Single DES:
DESCRIPTION
:var MODE_ECB: :ref:`Electronic Code Book (ECB) <ecb_mode>`
:var MODE_CBC: :ref:`Cipher-Block Chaining (CBC) <cbc_mode>`
:var MODE_CFB: :ref:`Cipher FeedBack (CFB) <cfb_mode>`
:var MODE_OFB: :ref:`Output FeedBack (OFB) <ofb_mode>`
:var MODE_CTR: :ref:`CounTer Mode (CTR) <ctr_mode>`
:var MODE_OPENPGP: :ref:`OpenPGP Mode <openpgp_mode>`
:var MODE_EAX: :ref:`EAX Mode <eax_mode>`
FUNCTIONS
new(key, mode, *args, **kwargs)
Create a new DES cipher.
:param key:
The secret key to use in the symmetric cipher.
It must be 8 byte long. The parity bits will be ignored.
:type key: bytes/bytearray/memoryview
:param mode:
The chaining mode to use for encryption or decryption.
:type mode: One of the supported ``MODE_*`` constants
:Keyword Arguments:
* **iv** (*byte string*) --
(Only applicable for ``MODE_CBC``, ``MODE_CFB``, ``MODE_OFB``,
and ``MODE_OPENPGP`` modes).
The initialization vector to use for encryption or decryption.
For ``MODE_CBC``, ``MODE_CFB``, and ``MODE_OFB`` it must be 8 bytes long.
For ``MODE_OPENPGP`` mode only,
it must be 8 bytes long for encryption
and 10 bytes for decryption (in the latter case, it is
actually the *encrypted* IV which was prefixed to the ciphertext).
If not provided, a random byte string is generated (you must then
read its value with the :attr:`iv` attribute).
* **nonce** (*byte string*) --
(Only applicable for ``MODE_EAX`` and ``MODE_CTR``).
A value that must never be reused for any other encryption done
with this key.
For ``MODE_EAX`` there are no
restrictions on its length (recommended: **16** bytes).
For ``MODE_CTR``, its length must be in the range **[0..7]**.
If not provided for ``MODE_EAX``, a random byte string is generated (you
can read it back via the ``nonce`` attribute).
* **segment_size** (*integer*) --
(Only ``MODE_CFB``).The number of **bits** the plaintext and ciphertext
are segmented in. It must be a multiple of 8.
If not specified, it will be assumed to be 8.
* **mac_len** : (*integer*) --
(Only ``MODE_EAX``)
Length of the authentication tag, in bytes.
It must be no longer than 8 (default).
* **initial_value** : (*integer*) --
(Only ``MODE_CTR``). The initial value for the counter within
the counter block. By default it is **0**.
:Return: a DES object, of the applicable mode.
DATA
MODE_CBC = 2
MODE_CFB = 3
MODE_CTR = 6
MODE_EAX = 9
MODE_ECB = 1
MODE_OFB = 5
MODE_OPENPGP = 7
block_size = 8
key_size = 8
FILE
/home/jyt/anaconda3/lib/python3.11/site-packages/Crypto/Cipher/DES.py
d = DES.new(b'azertyui', DES.MODE_ECB) # Clef de 64 bits = 8 caractères
x = b"Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.$$$$$"
print (len(x)) # doit être multiple de 8, d'où les $ ...
y = d.encrypt(x)
y
128
b"3pZWb\xc4\xea\xd0l\x00\xb4=\x9d$\xd7\x12U\xb9\xeb41\xe0\xc9\x0eCh\xa5Z~~\x1c\xefRT%{\xea\x9b\xfdB\x96\xfa]0;F\xf9O9\xd1$L+\xadk\xa6\xa2-[\xa1\xc9\x1a\xdfS\x1e\x97#^\xaf'\xa6\xd1\xfd'ZA\x9f\xa9\xe3\xb5\xf4\xdaR\xc90\x80\x8b\xce;\xa8b\xa8\xdb4\xe6\xcd\xf7\xf0s\xd5\x1e\xa1Z\x01\xddt\xbeb*\\\xd4q2\x16i\xe4\x01\x03\xebF\xaa\x06\xdc\xb8`&\xd2\xe9"
d.decrypt(y)
b'Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.$$$$$'
En plus de la clef, nous avons deux paramètres optionnels : le mode, et le vecteur d'initialisation.
Pour comprendre leur utilité, chiffrons une petite image (photographie d'un document secret) :

from PIL import Image
im = Image.open("x.png")
im.size, im.mode
((728, 90), 'RGBA')
s = im.tobytes()
t = d.encrypt(s)
Image.frombytes(im.mode,im.size,t).save('y.png')
Contemplons le résultat

Ce n'est pas brillant. Le problème vient du mode opératoire.
La manière naïve (chiffrer chaque bloc avec la même clé) est appelée mode ECB (Electronic Code Book). Évidemment, les blocs identiques sont chiffrés de manière identique, ce qui présente un risque certain.
Dans le mode CBC (Cipher Block Chaining), on applique sur chaque bloc un "OU exclusif" avec le chiffrement du bloc précédent avant qu’il ne soit lui-même chiffré.
d=DES.new(b'azertyui',2,IV=b'\0'*8) #IV obligatoire dans cette version
t=d.encrypt(s)
Image.frombytes(im.mode,im.size,t).save('z.png')
Contemplons le résultat :

On peut utiliser un autre vecteur d'initialisation, afin que deux messages identiques, bien que chiffrés avec la même clef, soient chiffrés de manière différente.
d=DES.new(b'azertyui',2, IV=b'blahblah')
t1=d.encrypt(s)
Image.frombytes(im.mode,im.size,t1).save('w.png')
On obtient

t[:40]
b'\xfe\xa1\xc5\xd2\xadqJ\x0c\xf5{\xfc\x0b*\xfb\xffV\xd5;M\x1d\xa3\xd3\x0c\xfc6F\x0e\x17\x9d\xa7@r\x14\x11%\x8c\xeb\x8e\xeaF'
t1[:40]
b']F\xe2w\xb9\xfc\xeb\xad\xec\x11\xf5\x01\xe6d7\x14A\x8f\x85\x1c\xe1\x8f\xc3\x0f\x1bY\xc3\x8b\xf1\xa1\x7fh\x84\xd9|\x92\xf7\xb6\xe4\xa3'
Réseaux de permutations-substitutions (SPN, Substitution-Permutation Networks)¶
Ils se composent d'un certain nombre $r$ d'étages (ou tours, rounds), qui opérent sur des blocs de $N$ bits.
Chaque étage se compose de S-boîtes (S-boxes) et d'une P-boîte (P-box).
Les S-boîtes calculent des fonctions arbitraires $\{0,1\}^k\rightarrow \{0,1\}^l$.
Les P-boîtes réalisent des permutations des bits.
Un SPN est caractérisé par
- son nombre $r$ d'étages
- Un algorithme de diversification de la clef : $K \rightarrow K_1,K_2,\ldots,K_r$ (clefs d'étage)
- Sa fonction d'étage $w_i = f(w_{i-1},K_{i-1})$ ($w_0$ est le texte clair, $w_r$ le texte chiffré).
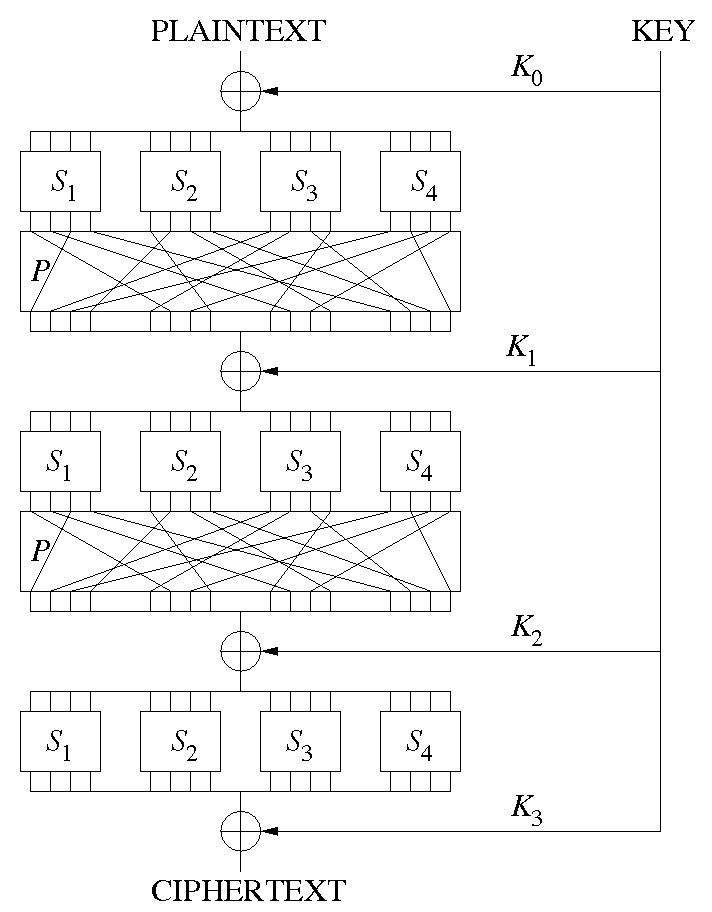
Structures de Feistel¶
Il s'agit d'une architecture facilitant la conception et l'implantation des SPN. Chiffrement et déchiffrement utilisent le même algorithme.
La sécurité d'un tel système dépend du choix de la fonction d'étage $f(x,y)$ (qui n'a pas besoin d'être injective), et de l'algorithme de diversification de la clé.
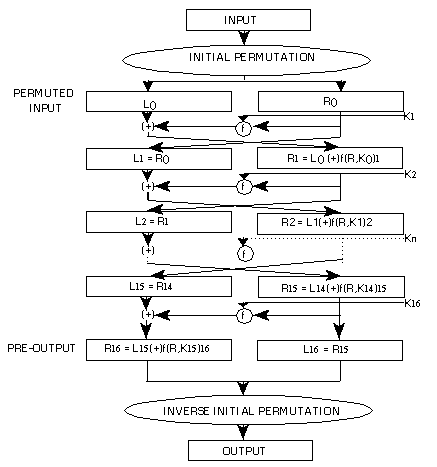
On travaille sur des blocs de longueur paire $N=2N'$ (pour le DES, $N=64$).
Conventions¶
Les blocs de texte clair (plaintext) sont notés $P$. On note $||$ l'opérateur de concaténation, et $\oplus$ l'opérateur de OU exclusif bit-à-bit.
Les blocs sont divisés en deux moitiés de $N'$ bits, $L$ et $R$.
Au départ, $P=L_0||R_0$.
Pour i de 1 à r :
a) calculer $R_i = L_i\oplus f(R_{i-1},K_i)$
b) $L_i = R_{i-1}$
Exemple¶
Pour chiffrer $P$, $${R_0\choose L_0}\rightarrow {R_1=L_0\oplus f(R_0,K_1)\choose L_1=R_0} \rightarrow {R_2=L_1\oplus f(R_1,K_2)\choose L_2=R_1} \rightarrow{R_3=L_2\oplus f(R_2,K_3)\choose L_3=R_2}$$ Pour déchiffrer, $${R_2=L_3\choose L_2=R_3\oplus f(R_2,K_3)}\rightarrow{R_1=L_2\choose L_1=R_2\oplus f(R_1,K_2)}\rightarrow{R_0=L_1\choose L_0=R_1\oplus f(R_0,K_1)}$$
Paramètres du DES¶
Blocs de $N=64$ bits, clef de 64 bits dont seulement 56 sont utilisés (les bits 8,16,24,32,40,48,56 sont des contrôles de parité).
Le nombre de clefs possible est $$2^{56} = 72.057.594.037.927.936$$
C'est beaucoup. Cependant, en 1998, l'EFF (Electronic Frontier Foundation) a pu construire une machine spécialisée, DES Cracker, dite DeepCrack pour seulement $ 250 000, permettant de retrouver une clef DES en 56 heures. On estime qu'en 1976, une telle machine aurait pu être construite pour 20 millions de dollars, une somme à la portée de la NSA.
Dans la description officielle, les bits sont numérotés de 1 à 64, le bit de poids fort en premier. Par exemple, $18=2^4+2^1={12345\choose 10010}$.
Nombre d'étages $r=16$.
Diversification de la clef On élimine les bits $8i$, $i=1,\ldots,8$. On obtient deux moitiés de 28 bits $K_0=C_0||D_0$.
Pour $i=1,2,9,16$, on calcule $$C_i = {\rm lrot}_1(C_{i-1}),\ D_i = {\rm lrot}_1(D_{i-1})$$ Pour $i=38,10-15$, $$C_i = {\rm lrot}_2(C_{i-1}),\ D_i={\rm lrot}_2(C_{i-2})$$ Les résultats $C_i||D_i$ sont filtrés par une permutation sélective. On obtient 16 clés d'étage de 48 bits.
Fonction d'étage Elle prend en entrée 32 bits, filtrés par une permutation expansive qui en produit 48. Il passent par 8 S-boîtes différentes, ayant chacune 6 bits en entrée et 4 bits en sortie. Les 32 bits sortants sont passés dans une P-boîte.
AES (Advanced Encryption Standard)¶
Issu d'un appel à candidatures international lancé en janvier 1997 et adopté par le NIST (National Institute of Standards and Technology) en 2001. Il utilise peu de mémoire. Il n'est pas basé sur un schéma de Feistel, sa complexité est moindre et il est plus facile à mettre en oeuvre.
L'algorithme prend en entrée un bloc de 128 bits (16 octets), la clé fait 128, 192 ou 256 bits. Les 16 octets en entrée sont permutés selon une table définie au préalable. Ces octets sont ensuite placés dans une matrice de 4x4 éléments et ses lignes subissent une rotation vers la droite. L'incrément pour la rotation varie selon le numéro de la ligne. Une transformation linéaire est ensuite appliquée sur la matrice, elle consiste en la multiplication binaire de chaque élément de la matrice avec des polynômes issus d'une matrice auxiliaire, à coefficients dans le corps fini ${\mathbb F}_{2^8}$
Finalement, un OU exclusif XOR entre la matrice et une autre matrice permet d'obtenir une matrice intermédiaire. Ces différentes opérations sont répétées plusieurs fois et définissent un « tour ». Pour une clé de 128, 192 ou 256, AES nécessite respectivement 10, 12 ou 14 tours.
On trouvera des détails ici.
from Crypto.Cipher import AES
help(AES)
Help on module Crypto.Cipher.AES in Crypto.Cipher:
NAME
Crypto.Cipher.AES - Module's constants for the modes of operation supported with AES:
DESCRIPTION
:var MODE_ECB: :ref:`Electronic Code Book (ECB) <ecb_mode>`
:var MODE_CBC: :ref:`Cipher-Block Chaining (CBC) <cbc_mode>`
:var MODE_CFB: :ref:`Cipher FeedBack (CFB) <cfb_mode>`
:var MODE_OFB: :ref:`Output FeedBack (OFB) <ofb_mode>`
:var MODE_CTR: :ref:`CounTer Mode (CTR) <ctr_mode>`
:var MODE_OPENPGP: :ref:`OpenPGP Mode <openpgp_mode>`
:var MODE_CCM: :ref:`Counter with CBC-MAC (CCM) Mode <ccm_mode>`
:var MODE_EAX: :ref:`EAX Mode <eax_mode>`
:var MODE_GCM: :ref:`Galois Counter Mode (GCM) <gcm_mode>`
:var MODE_SIV: :ref:`Syntethic Initialization Vector (SIV) <siv_mode>`
:var MODE_OCB: :ref:`Offset Code Book (OCB) <ocb_mode>`
FUNCTIONS
get_random_bytes = urandom(size, /)
Return a bytes object containing random bytes suitable for cryptographic use.
new(key, mode, *args, **kwargs)
Create a new AES cipher.
:param key:
The secret key to use in the symmetric cipher.
It must be 16, 24 or 32 bytes long (respectively for *AES-128*,
*AES-192* or *AES-256*).
For ``MODE_SIV`` only, it doubles to 32, 48, or 64 bytes.
:type key: bytes/bytearray/memoryview
:param mode:
The chaining mode to use for encryption or decryption.
If in doubt, use ``MODE_EAX``.
:type mode: One of the supported ``MODE_*`` constants
:Keyword Arguments:
* **iv** (*bytes*, *bytearray*, *memoryview*) --
(Only applicable for ``MODE_CBC``, ``MODE_CFB``, ``MODE_OFB``,
and ``MODE_OPENPGP`` modes).
The initialization vector to use for encryption or decryption.
For ``MODE_CBC``, ``MODE_CFB``, and ``MODE_OFB`` it must be 16 bytes long.
For ``MODE_OPENPGP`` mode only,
it must be 16 bytes long for encryption
and 18 bytes for decryption (in the latter case, it is
actually the *encrypted* IV which was prefixed to the ciphertext).
If not provided, a random byte string is generated (you must then
read its value with the :attr:`iv` attribute).
* **nonce** (*bytes*, *bytearray*, *memoryview*) --
(Only applicable for ``MODE_CCM``, ``MODE_EAX``, ``MODE_GCM``,
``MODE_SIV``, ``MODE_OCB``, and ``MODE_CTR``).
A value that must never be reused for any other encryption done
with this key (except possibly for ``MODE_SIV``, see below).
For ``MODE_EAX``, ``MODE_GCM`` and ``MODE_SIV`` there are no
restrictions on its length (recommended: **16** bytes).
For ``MODE_CCM``, its length must be in the range **[7..13]**.
Bear in mind that with CCM there is a trade-off between nonce
length and maximum message size. Recommendation: **11** bytes.
For ``MODE_OCB``, its length must be in the range **[1..15]**
(recommended: **15**).
For ``MODE_CTR``, its length must be in the range **[0..15]**
(recommended: **8**).
For ``MODE_SIV``, the nonce is optional, if it is not specified,
then no nonce is being used, which renders the encryption
deterministic.
If not provided, for modes other than ``MODE_SIV```, a random
byte string of the recommended length is used (you must then
read its value with the :attr:`nonce` attribute).
* **segment_size** (*integer*) --
(Only ``MODE_CFB``).The number of **bits** the plaintext and ciphertext
are segmented in. It must be a multiple of 8.
If not specified, it will be assumed to be 8.
* **mac_len** : (*integer*) --
(Only ``MODE_EAX``, ``MODE_GCM``, ``MODE_OCB``, ``MODE_CCM``)
Length of the authentication tag, in bytes.
It must be even and in the range **[4..16]**.
The recommended value (and the default, if not specified) is **16**.
* **msg_len** : (*integer*) --
(Only ``MODE_CCM``). Length of the message to (de)cipher.
If not specified, ``encrypt`` must be called with the entire message.
Similarly, ``decrypt`` can only be called once.
* **assoc_len** : (*integer*) --
(Only ``MODE_CCM``). Length of the associated data.
If not specified, all associated data is buffered internally,
which may represent a problem for very large messages.
* **initial_value** : (*integer* or *bytes/bytearray/memoryview*) --
(Only ``MODE_CTR``).
The initial value for the counter. If not present, the cipher will
start counting from 0. The value is incremented by one for each block.
The counter number is encoded in big endian mode.
* **counter** : (*object*) --
Instance of ``Crypto.Util.Counter``, which allows full customization
of the counter block. This parameter is incompatible to both ``nonce``
and ``initial_value``.
* **use_aesni** : (*boolean*) --
Use Intel AES-NI hardware extensions (default: use if available).
:Return: an AES object, of the applicable mode.
DATA
MODE_CBC = 2
MODE_CCM = 8
MODE_CFB = 3
MODE_CTR = 6
MODE_EAX = 9
MODE_ECB = 1
MODE_GCM = 11
MODE_OCB = 12
MODE_OFB = 5
MODE_OPENPGP = 7
MODE_SIV = 10
block_size = 16
key_size = (16, 24, 32)
FILE
/home/jyt/anaconda3/lib/python3.11/site-packages/Crypto/Cipher/AES.py
K = open('/dev/urandom','rb').read(16)
K
b'\xbb\x04>C\xaf\xb2:\xe9&#\xc2\xa4C|u\xc4'
A = AES.new(K,1)
msg = b'\x00'*128
msg
b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00'
A.encrypt(msg)
b'k\xe6\xe4\x92p\x81\x01\xa8\xed\xf8??\xaa\x94\x8f"k\xe6\xe4\x92p\x81\x01\xa8\xed\xf8??\xaa\x94\x8f"k\xe6\xe4\x92p\x81\x01\xa8\xed\xf8??\xaa\x94\x8f"k\xe6\xe4\x92p\x81\x01\xa8\xed\xf8??\xaa\x94\x8f"k\xe6\xe4\x92p\x81\x01\xa8\xed\xf8??\xaa\x94\x8f"k\xe6\xe4\x92p\x81\x01\xa8\xed\xf8??\xaa\x94\x8f"k\xe6\xe4\x92p\x81\x01\xa8\xed\xf8??\xaa\x94\x8f"k\xe6\xe4\x92p\x81\x01\xa8\xed\xf8??\xaa\x94\x8f"'
A = AES.new(K,AES.MODE_CBC, b'\xff'*16)
A.encrypt(msg)
b'\xea\x95/q)\xae\x83\xdf\xc4R\xac\x91\x98\xa32\x03\xeb9U\xffb\xd7\x05\xceOi"\xf0\xc4B\xf8f\xe7M\xe2\xea\xea\x10\x81;\x19\x9fz\xe3\xabd\x00L\x98Kld-?\x86\xdfi.]r\x9e\x05{\xa1\xdc\x8d\xfc\x1d\xc2/FN\xa8=\x0b\xec&\x95_r\xbd\x1bN\x17\xdb\xd6\xba^\xe8~\xff\xc4S\xf6u\xbc\x91\xc4\xe4D\xae\xd3\xf24\x1c\x81\xb3\xc5\xbe\xfc\xf3v\x8d\xd9\x9e\'\x19\xb1\xa3Jr>\xb8XY\x1f#\xda'
Modes opératoires¶
On note $E(P,K)$ la fonction de chiffrement d'un bloc $P$ avec la clef $K$, et $D(C,K)$ la fonction de déchiffrement.
ECB (Electronic Code Book)¶
Les blocs identiques sont chiffrés de la même manière $$C_i = E(P_i,K)$$$ Comme on l'a vu, c'est à éviter.
CBC (Cipher Block Chaining)¶
On effectue sur chaque bloc un ‘OU exclusif’ avec le chiffrement du bloc précédent avant de le chiffrer. On utilise un vecteur d'initialisation (IV), généralement aléatoire, comme premier bloc. $$C_0 = IV,\ C_i = E(C_{i-1}\oplus P_i,K)$$
CFB (Cipher Feedback)¶
C'est un chiffrement par flux : $$C_0=IV,\ C_i=P_i\oplus E(C_{i-1},K)$$
CTR (Counter)¶
On engendre un flux en chiffrant un compteur (une fonction $g(i)$). $$C_i = P_i\oplus E(IV+g(i))$$
OFB (Output Feedback)¶
Ce mode transforme un chiffrement par blocs en un chiffrement par flux synchrone, c'est à dire que le flux est indépendant du clair et du chiffré. Cette propriété facilite l'emplo de codes correcteurs d'erreurs. $$I_0=IV,\ O_i=E(I_i,K),\ I_i=O_{i-1},\ C_i=P_i\oplus O_i$$
PGP (OpenPGP CFB Mode)¶
C'est une variante du mode CFB imposée par openPGP. Voir RFC 4880.
A = AES.new(K,AES.MODE_CFB,IV=b'\xff'*16)
A.encrypt(msg)
b'\xea\xf0\xfah\xc8\xda\xdf\xd3\xf3\\\xb2\xda\xb7\xfc\xb9f:\xd8\xc1\x06\x02\xf8.Dd:\xc5\x9a\x08\x99\xe1\x17e\x14N4\xef7g\x06\x07\x1cA\xf8\x15I\xb5h>n&R=\xcc\xa5\x15\xa1\x18\xce\x97\x12o\x84\xe7\xf6\x84\xf9\xc2.V\xca\x9dz\x05\x1d\xcd\xc8R\xb5\xb9\xbf\x1aV\x19\xfc\x1ft@{\xf1H\x15\x98#=\xaanMZ\xba\xc2\x98\xe5\xa5\xe4\x9e.\xda\xfa0\xe3\xea^\x81[\xa0t\xd5k\x7f=ciF\xfa\xf6~('
from Crypto.Util import Counter
ctr = Counter.new(128, initial_value=42)
A = AES.new(K,AES.MODE_CTR,counter = ctr)
A.encrypt(msg)
b'c\x00\xbdh\xe3\xa5n&\xc9\x17\xc2?%/\x97 \x85\xe1n8\x19\x1aVy\xca\x98\xa4/G"\r\xa2\xab*\x90\xd2\xb9qh\x08}\xde\xff\xf31m\xec\xcb\xf4\x87\xae\xd4\xea\x99\xb0\'d\x1f\xd8\x16\xa8\xf0\x15W!+($\x7f\x89F\x1dv\xed\xc9\x86.w\x06\x04\xf2\x89\x89\xe7\x17\x90\x87\xbc\xa8\x9d\xf1\xc7c~u\xdd\xea\x0c\xe7NV\xba\x8d\xb2\tV!\x82\xae\xc8\\\xde\xde\x9cN\xe0Y\xbb\xc1\xc6G\xa6\x87\x00\x95\xd0q\xb7'
A = AES.new(K,AES.MODE_OFB,IV=b'\xff'*16)
A.encrypt(msg)
b'\xea\x95/q)\xae\x83\xdf\xc4R\xac\x91\x98\xa32\x03\xeb9U\xffb\xd7\x05\xceOi"\xf0\xc4B\xf8f\xe7M\xe2\xea\xea\x10\x81;\x19\x9fz\xe3\xabd\x00L\x98Kld-?\x86\xdfi.]r\x9e\x05{\xa1\xdc\x8d\xfc\x1d\xc2/FN\xa8=\x0b\xec&\x95_r\xbd\x1bN\x17\xdb\xd6\xba^\xe8~\xff\xc4S\xf6u\xbc\x91\xc4\xe4D\xae\xd3\xf24\x1c\x81\xb3\xc5\xbe\xfc\xf3v\x8d\xd9\x9e\'\x19\xb1\xa3Jr>\xb8XY\x1f#\xda'
Sécurité des chiffrements par blocs.¶
On distingue plusieurs niveaux d'attaque :
- Chiffré connu seul
- Clair connu
- Clair choisi
On a vu que la force brute (test de toutes les clefs possibles) était devenue possible sur les $2^{56}$ clefs du DES. Elle reste impraticable avec des clefs plus longues, mais il existe des techniques permettant de réduire l'espace des clefs possibles.
La cryptanalyse linéaire (Matsui 1992).¶
Cette technique s'applique aux réseaux de permutations-substitutions (SPN). C'est une attaque à texte clair connu. L'attaquant doit disposer d'un grand nombre de couples (X,Y) de textes clairs/textes chiffrés.
L'idée est de trouver une relation linéaire
$$X_{i_1}\oplus X_{i_2}\oplus\cdots\oplus Y_{j_1}\oplus Y_{j_2}\cdots = K_{l_1}\oplus K_{l_2}\oplus\cdots$$entre certains bits de l'entrée $X$, de la sortie $Y$ et de la clé $K$ qui ne soit pas aléatoire. Si les bits d'entrée et de sortie étaient des variables aléatoires indépendantes, un telle relation serait vérifiée en moyenne une fois sur deux (probabilité $\frac12$).
Supposons qu'on en connaisse une qui ait une probabilité $p$ aussi différente de $\frac12$ que possible.
Algorithme 1 de Matsui¶
- Collecter un grand nombre $N$ de couples $(X,Y)$
- Pour chaque couple, calculer le membre gauche de l'expression linéaire. Soit $T$ le nombre de résultats nuls.
- Si $T$ est plus grand que $N/2$ et si $p > \frac12$ , on conclut que le membre droit doit être 0
- Si $T< N/2$ et si $p < \frac12$ , on conclut encore que le membre droit est 0
- Dans les autres cas, on conclut que le membre droit est 1
Ce n'est pas très efficace, mais on peut faire mieux avec le même principe. On va cette fois tester toutes les valeurs possibles des bits de la clé concernés par le membre droit de la relation.
Algorithme 2 de Matsui¶
- Collecter un grand nombre $N$ de couples $(X,Y)$
- Pour chaque jeu de bits de clé candidats, on calcule une valeur $T$ égale au nombre de fois que la relation est vérifiée
- On sélectionne les candidats qui ont un $T$ le plus éloigné possible de $N/2$.
Pour mettre en oeuvre cette technique, il faut commencer par calculer des « approximations linéaires » des seuls éléments non linéaires du système, à savoir les S-boîtes.
Si $X$ et $Y$ sont l'entrée et la sortie de la S-boîte considérée, sa table d'approximation linéaire est une matrice $2^l\times 2^m$ dont l'entrée $(i,j)$ est $T(i,j)-2^{l-1}$, où $T(i,j)$ est le nombre de fois que la relation linéaire $X|i = Y|j$ codée par les bits 1 de $i$ et $j$ est vérifiée.
Voir ici pour plus de détails.
Le livre Modern Cryptanalysis de Christopher Swenson contient un exemple détaillé en Python.
La cryptanalyse différentielle¶
C'est une attaque à texte clair choisi. Voir ici. La cryptanalyse repose sur des paires de textes clairs qui ont une différence constante. L'opération de différence peut être définie de diverses manières, la Fonction OU exclusif est la plus courante. L'attaquant calcule ensuite les différences dans les textes chiffrés, afin d'en extraire des motifs pouvant indiquer un biais. Les différences en sortie du chiffrement sont nommées des différentielles.
Il est maintenant connu que le DES avait été modifié pour résister à cette attaque, alors qu'elle n'a été officiellement découverte qu'à la fin des années 80.
D'autres algorithmes, comme FEAL-4 ont pu être cassés par cette technique.
On trouvera une liste d'attaques ici.