We are interested in the notion of resemblance or similarity between two words x and y of length m and n respectively. A dual notion is to look at the distance between these two words.
A word
x =
x0x1···xm-1
of length m is a sequence of letters from an alphabet
![]() .
Thus, for 0 <= i <= m-1,
.
Thus, for 0 <= i <= m-1,
![]() .
.
The empty word denoted by
![]() has a null length:
has a null length:
![]() .
.
A function d is a distance between words if:
Several distances between words can be considered:
We are interested in a distance which enables to transform x into y using three kinds of basic operations: the substitution of a letter of x by a letter of y, the deletion of a letter of x or the insertion of a letter of y. A cost is associated to each of these operations and for each letter of the alphabet:
The general problem consists of finding a sequence of such basic operations to transform x into y minimizing the total cost of the operations used. The total cost is equal to the sum of the costs of each of the basic operations. This cost is a distance on the words if Sub is a distance on the letters.
We are trying to minimize the distance between x and y which is generally the same (but not always) than maximizing the similarity between these two words.
The solution is not necessarily unique.
A solution can be given as a sequence of basic operations of substitutions, deletions and insertions. It can also be given in a similar way by an alignment.
For two words x of length m and y of length n such as m <= n. An alignment denoted by
![]()
or
![]()
of length p is such that:
An aligned pair of the type
![]() with
with
![]() indicates the substitution of the letter a by the letter
b.
indicates the substitution of the letter a by the letter
b.
An aligned pair of the type
![]() with
with
![]() indicates the deletion of the letter a.
indicates the deletion of the letter a.
An aligned pair of the type
![]() with
with
![]() indicates the insertion of the letter b.
indicates the insertion of the letter b.
In an alignement or in an aligned pair, the symbol
![]() is often replaced by the symbol -.
is often replaced by the symbol -.
This problem can be easily stated in terms of graph.
Let G = (V,E) be a labelled and weighted graph with
an application
![]() which associates a cost to each edge of E and an application
which associates a cost to each edge of E and an application
![]() which associates an aligned pair to each edge of E.
The graph G is defined as follows:
which associates an aligned pair to each edge of E.
The graph G is defined as follows:
All the paths from (-1,-1) to (3,5) correspond to a different
alignment between x and y.
The thick edges correspond to the following alignment:
![]() .
.
It is only necessary to find a shortest path from the vertex (-1,-1) to the vertex (m-1,n-1). The less the cost the less distant are the two words x and y. As the graph G is acyclic it is possible to find a shortest path considering one time and only one each vertex. One had just to consider them in a topological order. Such an order can be obtained by considering the vertices row by row and from left to right within each row. Dynamic programming ([3]) can solve this problem.
Let T be a two-dimensional table with m+1 rows and n+1 columns. The value of each square T[i,j], for -1 <= i <= m-1 and -1 <= j <= n-1 depends only on the three squares T[i-1,j], T[i,j-1] and T[i-1,j-1].
Then for 0 <= i <= m-1 and 0 <= j <= n-1, T[i,j] is the minimum cost of a path from (-1,-1) to (i,j). The algorithm DYNAMIC-PROGRAMMING computes all the values of the table T.
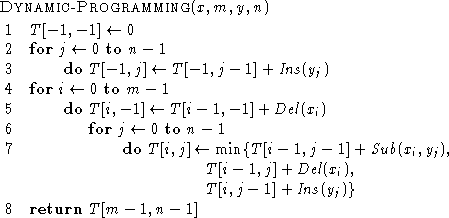
The algorithm DYNAMIC-PROGRAMMING clearly has a O(mn) time complexity.
The algorithm DYNAMIC-PROGRAMMING only computes the cost of the transformation of x into y. To get a sequence of basic operations to transform x into y or the corresponding alignment one has to trace back in the table T from square T[m-1,n-1] to square T[-1,-1] taking each time the right edge (see algorithm ONE-ALIGNMENT).
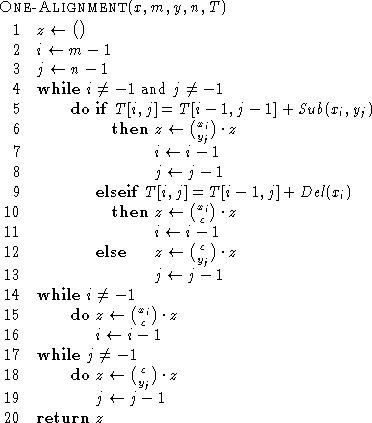
If all the optimal alignments are required then a call to
ALL-ALIGNMENT(x,
m-1,y,n-1,
![]() ,T)
will produced them.
,T)
will produced them.
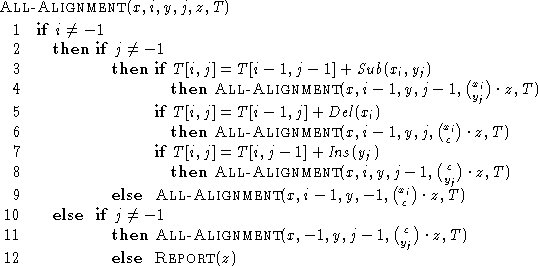
In this case it is necessary to store all the values of the table T then this problem can be solve in O(mn) space complexity.
When only the cost of the transformation of x into y is needed it is easy to see that a space in O(min(m,n)) is sufficient since the computation of a row (respectively a column) only needs the values of the previous row (respectively column).
Furthermore it is possible to compute an alignment in linear space
using a ``divide and conquer'' method
([9],
[11] and
[13]).