- variant of the Quick Search algorithm;
- requires the frequencies of the characters;
- preprocessing phase in O(m2+
 ) time and O(m+
) time and O(m+ ) space complexity;
) space complexity; - searching phase in O(mn) time complexity.




 ) time and O(m+
) time and O(m+ ) space complexity;
) space complexity;Sunday designed an algorithm where the pattern characters are scanned from the least frequent one to the most frequent one. Doing so one may hope to have a mismatch most of the times and thus to scan the whole text very quickly. One needs to know the frequencies of each of the character of the alphabet.
The preprocessing phase of the Optimal Mismatch algorithm consists in sorting the pattern characters in decreasing order of their frequencies and then in building the Quick Search bad-character shift function (see chapter Quick Search algorithm) and a good-suffix shift function adapted to the scanning order of the pattern characters. It can be done in O(m2+ ) time and O(m+
) time and O(m+ ) space complexity.
) space complexity.
The searching phase of the Optimal Mismatch algorithm has a O(mn) time complexity.
The function preQsBc is given chapter Quick Search algorithm.
typedef struct patternScanOrder {
int loc;
char c;
} pattern;
int freq[ASIZE];
/* Construct an ordered pattern from a string. */
void orderPattern(char *x, int m, int (*pcmp)(),
pattern *pat) {
int i;
for (i = 0; i <= m; ++i) {
pat[i].loc = i;
pat[i].c = x[i];
}
qsort(pat, m, sizeof(pattern), pcmp);
}
/* Optimal Mismatch pattern comparison function. */
int optimalPcmp(pattern *pat1, pattern *pat2) {
float fx;
fx = freq[pat1->c] - freq[pat2->c];
return(fx ? (fx > 0 ? 1 : -1) :
(pat2->loc - pat1->loc));
}
/* Find the next leftward matching shift for
the first ploc pattern elements after a
current shift or lshift. */
int matchShift(char *x, int m, int ploc,
int lshift, pattern *pat) {
int i, j;
for (; lshift < m; ++lshift) {
i = ploc;
while (--i >= 0) {
if ((j = (pat[i].loc - lshift)) < 0)
continue;
if (pat[i].c != x[j])
break;
}
if (i < 0)
break;
}
return(lshift);
}
/* Constructs the good-suffix shift table
from an ordered string. */
void preAdaptedGs(char *x, int m, int adaptedGs[],
pattern *pat) {
int lshift, i, ploc;
adaptedGs[0] = lshift = 1;
for (ploc = 1; ploc <= m; ++ploc) {
lshift = matchShift(x, m, ploc, lshift, pat);
adaptedGs[ploc] = lshift;
}
for (ploc = 0; ploc <= m; ++ploc) {
lshift = adaptedGs[ploc];
while (lshift < m) {
i = pat[ploc].loc - lshift;
if (i < 0 || pat[ploc].c != x[i])
break;
++lshift;
lshift = matchShift(x, m, ploc, lshift, pat);
}
adaptedGs[ploc] = lshift;
}
}
/* Optimal Mismatch string matching algorithm. */
void OM(char *x, int m, char *y, int n) {
int i, j, adaptedGs[XSIZE], qsBc[ASIZE];
pattern pat[XSIZE];
/* Preprocessing */
orderPattern(x, m, optimalPcmp, pat);
preQsBc(x, m, qsBc);
preAdaptedGs(x, m, adaptedGs, pat);
/* Searching */
j = 0;
while (j <= n - m) {
i = 0;
while (i < m && pat[i].c == y[j + pat[i].loc])
++i;
if (i >= m)
OUTPUT(j);
j += MAX(adaptedGs[i],qsBc[y[j + m]]);
}
}
Preprocessing phase
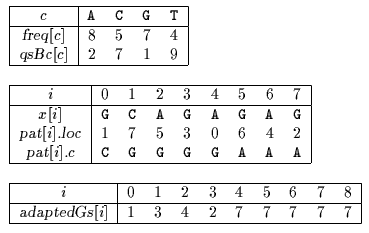
Tables used by Optimal Mismatch algorithm.
Searching phase



