List *z;
#define getZ(i) z[(i)]
void setZ(int node, int i) {
List cell;
cell = (List)malloc(sizeof(struct _cell));
if (cell == NULL)
error("ALPHASKIP/setZ");
cell->element = i;
cell->next = z[node];
z[node] = cell;
}
/* Create the transition labelled by the
character c from node node.
Maintain the suffix links accordingly. */
int addNode(Graph trie, int art, int node, char c) {
int childNode, suffixNode, suffixChildNode;
childNode = newVertex(trie);
setTarget(trie, node, c, childNode);
suffixNode = getSuffixLink(trie, node);
if (suffixNode == art)
setSuffixLink(trie, childNode, node);
else {
suffixChildNode = getTarget(trie, suffixNode, c);
if (suffixChildNode == UNDEFINED)
suffixChildNode = addNode(trie, art,
suffixNode, c);
setSuffixLink(trie, childNode, suffixChildNode);
}
return(childNode);
}
void ALPHASKIP(char *x, int m, char *y, int n, int a) {
int b, i, j, k, logM, temp, shift, size, pos;
int art, childNode, node, root, lastNode;
List current;
Graph trie;
logM = 0;
temp = m;
while (temp > a) {
++logM;
temp /= a;
}
if (logM == 0) logM = 1;
/* Preprocessing */
size = 2 + (2*m - logM + 1)*logM;
trie = newTrie(size, size*ASIZE);
z = (List *)calloc(size, sizeof(List));
if (z == NULL)
error("ALPHASKIP");
root = getInitial(trie);
art = newVertex(trie);
setSuffixLink(trie, root, art);
node = newVertex(trie);
setTarget(trie, root, x[0], node);
setSuffixLink(trie, node, root);
for (i = 1; i < logM; ++i)
node = addNode(trie, art, node, x[i]);
pos = 0;
setZ(node, pos);
pos++;
for (i = logM; i < m - 1; ++i) {
node = getSuffixLink(trie, node);
childNode = getTarget(trie, node, x[i]);
if (childNode == UNDEFINED)
node = addNode(trie, art, node, x[i]);
else
node = childNode;
setZ(node, pos);
pos++;
}
node = getSuffixLink(trie, node);
childNode = getTarget(trie, node, x[i]);
if (childNode == UNDEFINED) {
lastNode = newVertex(trie);
setTarget(trie, node, x[m - 1], lastNode);
node = lastNode;
}
else
node = childNode;
setZ(node, pos);
/* Searching */
shift = m - logM + 1;
for (j = m + 1 - logM; j < n - logM; j += shift) {
node = root;
for (k = 0; node != UNDEFINED && k < logM; ++k)
node = getTarget(trie, node, y[j + k]);
if (node != UNDEFINED)
for (current = getZ(node);
current != NULL;
current = current->next) {
b = j - current->element;
if (x[0] == y[b] &&
memcmp(x + 1, y + b + 1, m - 1) == 0)
OUTPUT(b);
}
}
free(z);
}
 (m) of the pattern;
(m) of the pattern; (m).(n / (m-log
(m).(n / (m-log (m)))) expected text character comparisons.
(m)))) expected text character comparisons.


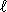 =log
=log (n-
(n-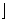 ].
].