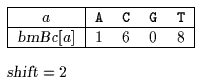
bmBc table used by Tuned Boyer-Moore algorithm.




The Tuned Boyer-Moore is a implementation of a simplified version of the Boyer-Moore algorithm which is very fast in practice. The most costly part of a string-matching algorithm is to check whether the character of the pattern match the character of the window. To avoid doing this part too often, it is possible to unrolled several shifts before actually comparing the characters. The algorithm used the bad-character shift function to find x[m-1] in y and keep on shifting until finding it, doing blindly three shifts in a row. This required to save the value of bmBc[x[m-1]] in a variable shift and then to set bmBc[x[m-1]] to 0. This required also to add m occurrences of x[m-1] at the end of y. When x[m-1] is found the m-1 other characters of the window are checked and a shift of length shift is applied.
The comparisons between pattern and text characters during each attempt can be done in any order. This algorithm has a quadratic worst-case time complexity but a very good practical behaviour.
The function preBmBc is given chapter Boyer-Moore algorithm.
void TUNEDBM(char *x, int m, char *y, int n) {
int j, k, shift, bmBc[ASIZE];
/* Preprocessing */
preBmBc(x, m, bmBc);
shift = bmBc[x[m - 1]];
bmBc[x[m - 1]] = 0;
memset(y + n, x[m - 1], m);
/* Searching */
j = 0;
while (j < n) {
k = bmBc[y[j + m -1]];
while (k != 0) {
j += k; k = bmBc[y[j + m -1]];
j += k; k = bmBc[y[j + m -1]];
j += k; k = bmBc[y[j + m -1]];
}
if (memcmp(x, y + j, m - 1) == 0 && j < n)
OUTPUT(j);
j += shift; /* shift */
}
}
Preprocessing phase
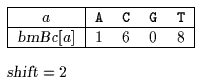
bmBc table used by Tuned Boyer-Moore algorithm.
Searching phase



