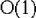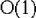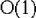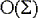Implements |
DFA |
Class Specifications |
| name |
DFA_matrix |
| template parameters |
class _Sigma = Type_alphabet<char>,
class _Tag = empty_tag,
ifndef WIN32 class Allocator = default_allocator |
| constructor |
WIN32:
DFA_matrix(unsigned long = 0)
else:
DFA_matrix(unsigned long = 0, Allocator a = Allocator()) |
|
File |
dfa_matrix.h |
Structure |
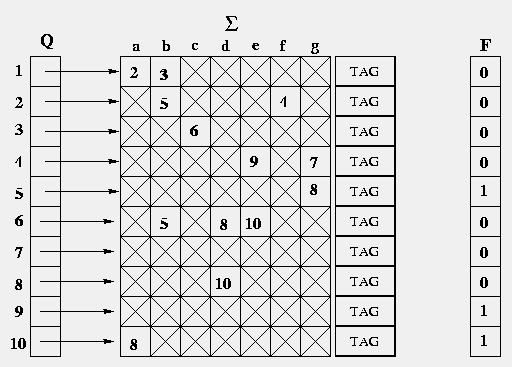
It is the most natural way to implement the set of transitions. It makes use of a (number of states * size of Sigma) matrix built from a container of pointers to pair of tag and vector of size |Sigma| holding aims of a particular state. F is a bit vector.
 |
time |
Add state: amortized 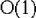
Remove state: 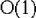
Add/Remove/Access transition: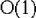
Iteration on edges: 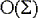 |
Space |
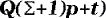 |
Use Cases |
This is the fastest data structure except for the edges traversal. All operations are processed in constant time. On the other hand, it demands O(Q*Sigma) memory space which is particularly inefficient on big automata with large alphabets. Moreover, it requires a finite alphabet, a mapping from Sigma to integers and a dense matrix to avoid memory space waste.
Typical use of this class are pattern matching and regular expressions implementations where automata keep relativel small and fast retrieval of transitions is crucial.
It is not recommended to use it when iteration on the outgoing transitions of states is intensively used since it is in O(Sigma) time, unless the matrix is dense. |