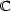 n est un ensemble de sous espaces affines P = {Eki} dont les dimensions k (notées en indice) sont
strictement inférieures à n et ayant certaines propriétés.
n est un ensemble de sous espaces affines P = {Eki} dont les dimensions k (notées en indice) sont
strictement inférieures à n et ayant certaines propriétés.
Un polytope de 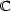 n est un ensemble de sous espaces affines P = {Eki} dont les dimensions k (notées en indice) sont
strictement inférieures à n et ayant certaines propriétés.
n est un ensemble de sous espaces affines P = {Eki} dont les dimensions k (notées en indice) sont
strictement inférieures à n et ayant certaines propriétés.
Avant de les donner, nous avons besoin de quelques définitions intermédiaires. On dit que deux sous espaces Ek et
Ek' sont incidents si l’un est sous-espace propre de l’autre (Ek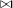 Ek'). Deux espaces Ek et Ek' sont connectés dans P si
il existe une chaîne d’éléments de P vérifiant
Ek'). Deux espaces Ek et Ek' sont connectés dans P si
il existe une chaîne d’éléments de P vérifiant
 | (1) |
On dira que P est connexe si tout couple d’espaces est connecté.
Pour tout couple d’espaces incidents (Ek,Ek') (k < k'), la figure intermédiaire est le sous ensemble de P:
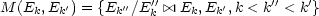 | (2) |
Une configuration P est un polytope si et seulement si les deux assertions suivantes sont vérifiées
Parmis les polytopes, il en existe certains de remarquables: les polytopes réguliers dont voici la définition donnée par Shephard.
Un polytope est régulier si les trois conditions sont respectées
Tout polytope P admet un groupe de reflection GP, qui est un sous-groupe du groupe symétrique, échangeant les sommets et préservant l’arrangements des espaces3. Ce groupe est appelé groupe de symétrie ou groupe des automorphismes du polytope.
Un drapeau est un n-uplet (P0,P1,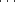 ,Pn-1)
,Pn-1)  Pn (P0 dim 0
Pn (P0 dim 0 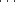 ) de
sous-polytopes4.
) de
sous-polytopes4.
Coxeter donne une définition alternative des polytopes réguliers utilisant les drapeaux: un polytope est régulier si et seulement si son groupe de symétrie est transitif sur les drapeaux.
Cette définition est pratique car elle va nous permettre de calculer les groupes de symétrie, une propriété remarquable étant que l’ordre du groupe est égal au nombre de drapeaux.
Soit k < n et P0,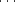 Pk-1,Pk+1,
Pk-1,Pk+1, ,Pn-1. La définition des polytopes implique qu’il existe deux
drapeaux
,Pn-1. La définition des polytopes implique qu’il existe deux
drapeaux
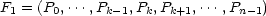

La transformation tk laisse invariant les centres5
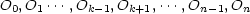
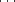 ,Pk-1,Pk+1,
,Pk-1,Pk+1,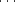 ,Pn-1,P. En fait tout l’hyperplan Mk contenant ces n+1 points est invariant. La transformation tk est donc
une pseudo-reflection 6
de miroir Mk. Considérons le sous groupe Gk du groupe de symétrie laissant invariant les sous-polytopes de degrés
différents de k dans un drapeau donné. Toutes ses reflections ont le même miroir et sont engendrées par une reflection
Rk+1. Nous noterons pk+1 sa période (Rk+1pk+1 = Id) qui est égale au nombre d’élements de la figure intermédiaire de
Pk-1 et Pk+1. Peter McMullen a montré en 1967 que le groupe de symétrie pouvait être engendré par les reflections R1,
R2,
,Pn-1,P. En fait tout l’hyperplan Mk contenant ces n+1 points est invariant. La transformation tk est donc
une pseudo-reflection 6
de miroir Mk. Considérons le sous groupe Gk du groupe de symétrie laissant invariant les sous-polytopes de degrés
différents de k dans un drapeau donné. Toutes ses reflections ont le même miroir et sont engendrées par une reflection
Rk+1. Nous noterons pk+1 sa période (Rk+1pk+1 = Id) qui est égale au nombre d’élements de la figure intermédiaire de
Pk-1 et Pk+1. Peter McMullen a montré en 1967 que le groupe de symétrie pouvait être engendré par les reflections R1,
R2, 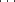 , Rn laissant respectivement invariants les hyperplans engendrés par les points O1
, Rn laissant respectivement invariants les hyperplans engendrés par les points O1 On,
On,  O0
O0 On-1 où les
Oi sont les centres de polytopes Pi tels que D = (P0,P1,
On-1 où les
Oi sont les centres de polytopes Pi tels que D = (P0,P1,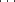 ,Pn) soit un drapeau. Les n lignes O0O1,
,Pn) soit un drapeau. Les n lignes O0O1, 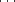 , On-1On
sont deux à deux orthogonales ainsi que les miroirs Mk et Mk' lorsque k < k'- 1. Les pseudo-reflections Rk et Rk'
commutent donc. Les groupes de symétrie des polytopes sont engendrés par des reflections satisfaisant les relations
, On-1On
sont deux à deux orthogonales ainsi que les miroirs Mk et Mk' lorsque k < k'- 1. Les pseudo-reflections Rk et Rk'
commutent donc. Les groupes de symétrie des polytopes sont engendrés par des reflections satisfaisant les relations

 | (5) |
où le nombre de termes à gauche et à droite du signe = est le même (on le notera qi).
Les polytopes sont codés par p1{q1}p2{q2}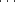 pn-1{qn-1}pn et leur groupe par p1[q1]p2[q2]
pn-1{qn-1}pn et leur groupe par p1[q1]p2[q2]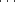 pn-1[qn-1]pn.
pn-1[qn-1]pn.
Si on considère un polytope régulier p1{q1}p2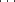 pn-1{qn-1}pn. Les droites O0O1,
pn-1{qn-1}pn. Les droites O0O1,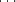 ,On-1On sont orthogonales. Les
miroirs Mk et Mk' sont orthogonaux pour k < k'- 1. Entre les miroirs Mk et Mk+1 il y a un angle
,On-1On sont orthogonales. Les
miroirs Mk et Mk' sont orthogonaux pour k < k'- 1. Entre les miroirs Mk et Mk+1 il y a un angle  k qui dépend de
pk, pk' et qk:
k qui dépend de
pk, pk' et qk:
 | (6) |
On considère les n miroirs M1,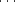 ,Mn que l’on a construit précédement. Ce sont des hyperplans vectoriels et sont donc
complétement définis par la donnée de leur vecteurs normaux e1,
,Mn que l’on a construit précédement. Ce sont des hyperplans vectoriels et sont donc
complétement définis par la donnée de leur vecteurs normaux e1, ,en. Ces vecteurs forment une base de
,en. Ces vecteurs forment une base de 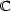 n qui n’est
pas orthogonale. En effet, si lorsque m < n - 1, on a bien l’orthogonalité de em et en, par contre lorsque on a
m = n - 1, les deux vecteurs forment un angle de
n qui n’est
pas orthogonale. En effet, si lorsque m < n - 1, on a bien l’orthogonalité de em et en, par contre lorsque on a
m = n - 1, les deux vecteurs forment un angle de  +
+  m. Soit
m. Soit
 | (7) |
un vecteur de 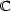 n. Son carré scalaire est
n. Son carré scalaire est
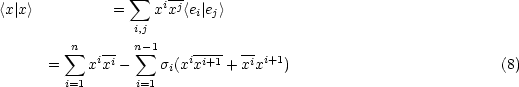
 uifi:
uifi:
 | (9) |
Les miroirs sont données alors par les équations
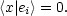 | (10) |
Éxprimées en fonction des ui: si on a ui =  j=1n
j=1n ijxj, alors les miroirs ont pour équations
ijxj, alors les miroirs ont pour équations
 | (11) |
Chacune des pseudo-reflections Rl agit de la façon suivante
 | (12) |
Pour construire l’ensemble des sommets, il suffit d’en trouver un et de calculer son orbite par le groupe de symétrie du polytope. C’est à dire de faire agir sur le sommet toutes les transformations obtenues en composant les pseudo-reflections Ri calculée au paragraphe précédent. On peut trouver un sommet en le choisissant dans l’intersection de tous les miroirs de symétrie sauf le premier.
Pour les arêtes le principe est le même: on trouve une arête et on calcule son orbite. Pour trouver une arête, il suffit de partir du premier sommet calculé et de calculer son orbite par les transformations engendrées par R1 uniquement.
On peut recommencer pour les faces (si le polytope est au moins de dimension 3) . On trouve une face en calculant l’orbite du premier sommet calculé par les transformations engendrées uniquement par R1 et R2 puis on calcule l’orbite de la face en faisant agir toutes les transformations... Et on continue, si le polytope est de dimension supérieure.
Nous allons suivre la méthode expliquée au paragraphe précédent. Pour se faire, nous allons choisir un système de calcul formel (par exemple Maple) ou bien prendre une feuille de papier et un crayon et s’armer de beaucoup de patience.
Les polygones complexes n’ont que deux miroirs de reflections, donc leur groupe de symétrie n’est engendrée que par deux pseudo-reflections que l’on notera R1 et R2.
Imaginons que nous voulions calculer le polygone complexe p1{q1}p2 (en supposant que cela forme un polygone, c’est à dire que le groupe de symétrie engendré par R1 et R2 soit fini). Nous allons commencer par calculer l’angle formé par les deux miroirs.
>l:=sqrt((cos(Pi/p1-Pi/p2)+cos(2*Pi/q1))/(2*sin(Pi/p1)*sin(Pi/p2)));
|
Ici on a l = cos 1. La forme Hermitienne invariante est
1. La forme Hermitienne invariante est

D’où on déduit les équations des miroirs puis les transformations R1 et R2. Ce qui se programme de la façon suivante
> e:=transpose(matrix(2,2,[-1,l,0,sqrt(1-l^2)]));
> eb:=transpose(e); > R1:=proc(U) [U[1]+(exp(2*Pi*I/p1)-1)*e[1,1]* (eb[1,1]*U[1]+eb[2,1]*U[2]),U[2]+(exp(2*Pi*I/p1)-1)* e[1,2]*(eb[1,1]*U[1]+eb[2,1]*U[2])];map(expand,");end; > R2:=proc(U) [U[1]+(exp(2*Pi*I/p2)-1)*e[2,1]*(eb[1,2] *U[1]+eb[2,2]*U[2]),U[2]+(exp(2*Pi*I/p2)-1)*e[2,2]* (eb[1,2]*U[1]+eb[2,2]*U[2])];map(expand,");end; |
Pour calculer les sommets, il faut commencer par choisir un point dans le second miroir.
>sommets:={[normal(sqrt(1-l^2)),-l]};
|
Puis de calculer son orbite
>for i to 10 do
sommets:=sommets union map(R1,sommets) union map(R2,sommets); sommets:=map(x->map(expand,x),sommets); print(nops(sommets)); od: |
Cette dernière opération est à recommencer jusqu’à ce que le nombre de sommets ne varie plus. Attention, toutes fois, pour certains polygones, des plus compliqués, Maple n’est pas capable d’éxprimer sous une forme normale convenable les expressions trouvées. C’est notamment le cas lorsqu’il y a des racines sous les racines. Ceci impose alors de trouver plus de points que le nombre de sommets du polytope ou bien de remplacer expand par une fonction plus adéquate.
Pour trouver une arêtes nous partons toujours du même sommet.
>s:=[sqrt(1-l^2),-l];
|
Et nous calculons l’orbite de celui-ci par la transformation R1.
>UneArete:=[s];
>for i to p1-1 do s:=R1(s); UneArete:=[op(UneArete),s]; od |
Une arête contient nécessairement p1 sommets car R1 est de période P1.
Maintenant, nous pouvons calculer l’ensemble des arêtes. Cela se fait de la même façon que pour le calcul des sommets à un détail près: Une arête étant représentée comme une liste de sommets en utilisant union on risque d’ajouter des arêtes semblables plusieurs fois en ayant permuté l’ordre des sommets. C’est la raison pour laquelle, on utilise a programmé la fonction ajouter.
>aj:=proc(aaj,ens) local ens2;
ens2:=map(x->map(expand,x),map(convert,ens,set) union {{op(aaj)}}); if nops(ens2)>nops(ens) then ens union{aaj}; else ens; fi; end; >ajouter:=proc(ens1,ens2) E1:=ens1; for s in ens2 do E1:=aj(s,E1); od; E1; end; |
On peut enfin calculer l’orbite:
> Aretes:={UneArete};
> for i to 10 do Aretes:=ajouter(Aretes,map(x->map(R1,x),Aretes)); Aretes:=ajouter(Aretes, map(x->map(R2,x),Aretes)); Aretes:=map(x->map(y->map(expand,y),x),Aretes); print(nops(Aretes)); od: |
On itère la dernière opération jusqu’à ce que le nombre d’arêtes soit stable (cependant la remarque faite pour le calcul des sommets reste valable).
Notre polygone est enfin décrit. Mais ce n’est pas encore suffisant pour pouvoir le dessiner. Les coordonnées des
sommets sont dans 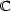 2 et il faut les projeter dans
2 et il faut les projeter dans 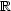 2. La technique est la suivante: on commence par les projeter sur une
droite de
2. La technique est la suivante: on commence par les projeter sur une
droite de 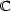 2 (ce qui revient à calculer une combinaison linéaire des coordonnées) puis on passe de
2 (ce qui revient à calculer une combinaison linéaire des coordonnées) puis on passe de 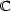 à
à 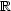 en dissociant la
partie réelle et la partie imaginaire. Le choix de la droite dépend de ce que l’on veut illustrer. Les projections ont été
choisies ici pour coller le plus possible au livre de Coxeter [1] lorsque le polytope est illustré sinon pour que les sommets
soient placés sur des cercles concentriques en essayant de respecter les relations de symétrie du polytope. Si
les projections calculées dans pst-coxcoor ne vous conviennent pas c’est la fonction Trans qu’il faut
changer.
en dissociant la
partie réelle et la partie imaginaire. Le choix de la droite dépend de ce que l’on veut illustrer. Les projections ont été
choisies ici pour coller le plus possible au livre de Coxeter [1] lorsque le polytope est illustré sinon pour que les sommets
soient placés sur des cercles concentriques en essayant de respecter les relations de symétrie du polytope. Si
les projections calculées dans pst-coxcoor ne vous conviennent pas c’est la fonction Trans qu’il faut
changer.
> Trans:=proc(U) local a,b, V;
a :=...; b :=..., V :=expand(a*U[1]+b*U[2]); [Re(V), Im(V)]; end; |
Pour calculer les coordonnées 2D des sommets, il suffit alors d’écrire:
>sommets2D:=convert(evalf(map(Trans,sommets)),list):
|
Vous pouvez alors les dessinez
>plot(sommets2D,style=point,axes=none);
|
De même vous pouvez calculer les arêtes en 2D
>aretes2D:=evalf(map(x->map(Trans,x),aretes)):nops(");
|
Et les dessiner
>display(polygonplot(convert(map(convert,aretes2D,list),list)),axes=none);
|
En sauvant la variable aretes2D dans un fichier et le retravaillant grâce à un traitement de texte, vous pouvez assez rapidement générer un des fichiers .dat utilisé par pst-coxcoor.
Ce sont les polygone réels classiques, ils ne sont pas implémentés ici.
Voir le package pst-coxparam
Ce sont deux polygones réciproques.

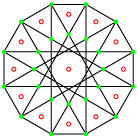
Leur groupe de symétrie est le 3[6]2 d’ordre 48. Le premier possède 16 sommets et 24 arêtes de deux sommets et le second 24 sommets et 16 arêtes de trois sommets. La projection utilisée ici est
>Trans:=proc(U)
V:=expand(U[1]+(exp(-I*Pi)+1)/sqrt(2)*U[2]); [Re(V),Im(V)]; end; |
C’est un polygone autodual (égal à son réciproque à une isométrie près).
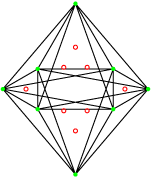
Son groupe de symétrie est le 3[3]3 d’ordre 24. Il possède 8 sommets et 8 arêtes de trois sommets. La projection utilisée est
>Trans:=proc(U)
V:=expand(U[1]+(exp(-I*Pi+1))/sqrt(2)*U[2]); [Re(V),Im(V)]; end; |
Ce sont deux polygones réciproques.
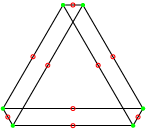
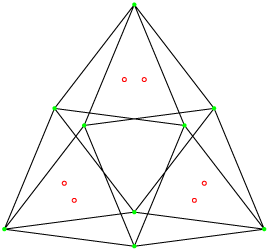
Leur groupe de symétrie est le 3[4]2 d’ordre 18. Le premier possède 6 sommets et 9 arêtes de deux sommets et le second 9 sommets et 6 arêtes de trois sommets. La projection utilisée ici est
>Trans:=proc(U)
dec:=Pi/6; V:=expand((U[1]+U[2]*exp(I*(dec)))*exp(I*Pi+Pi*I/24)); [Re(V),Im(V)]; end; |
Ce sont deux polygones réciproques.
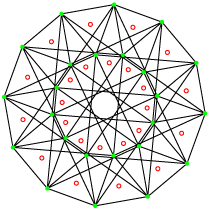
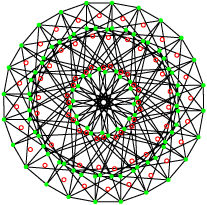
Leur groupe de symétrie est le 4[4]3 d’ordre 288. Le premier possède 72 sommets et 96 arêtes de trois sommets et le second 96 sommets et 72 arêtes de quatre sommets. La projection utilisée ici est
>Trans:=proc(U) local a, V;
a := -Pi/25; V :=expand(U[1]*exp(I*a)+(exp(I*(-Pi/25+a))+2)*U[2]); [Re(V), Im(V)]; end; |
C’est un polygone autodual (égal à son réciproque à une isométrie près).

Son groupe de symétrie est le 3[4]3 d’ordre 72. Il possède 24 sommets et 24 arêtes de trois sommets. La projection utilisée est
>Trans:=proc(U) local a, V;
a := -Pi/9; V := expand(U[1]*exp(I*a)+(exp(I*(-Pi/9+a))+1)*U[2])/sqrt(2); [Re(V), Im(V)]; end; |
C’est un polygone autodual (égal à son réciproque à une isométrie près).
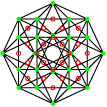
Son groupe de symétrie est le 4[3]4 d’ordre 96. Il possède 24 sommets et 24 arêtes de quatre sommets. La projection utilisée est
>Trans:=proc(U) local a, V;
a :=Pi/9; V := expand(U[1]*exp(I*a)+exp(I*(-2*Pi/9+a))*U[2]); [Re(V), Im(V)]; end; |
Ce sont deux polygones réciproques.

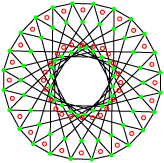
Leur groupe de symétrie est le 3[8]2 d’ordre 144. Le premier possède 48 sommets et 72 arêtes de deux sommets et le second 72 sommets et 48 arêtes de trois sommets. La projection utilisée ici est
>Trans:=proc(U) local V;
V :=expand(U[1])+(exp(I*(-Pi/48))+5/2)/sqrt(3)*U[2]); [Re(V), Im(V)]; end; |
C’est un polygone autodual (égal à son réciproque à une isométrie près).
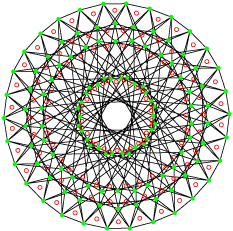
Son groupe de symétrie est le 3[5]3 d’ordre 360. Il possède 120 sommets et 120 arêtes de trois sommets. La projection utilisée est
>Trans:=proc(U) local a, V;
a := -Pi/25; V := expand(U[1]*exp(I*a)+(exp(I*(-Pi/25+a))+2)*U[2]); [Re(V), Im(V)]; end; |
Ce sont deux polygones réciproques.
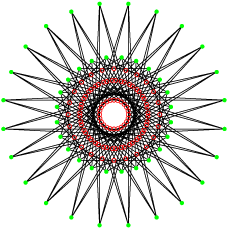

Leur groupe de symétrie est le 4[6]2 d’ordre 92. Le premier possède 96 sommets et 48 arêtes de deux sommets et le second 48 sommets et 96 arêtes de quatre sommets. La projection utilisée ici est
>Trans:=proc(U)
V:=expand(U[2]+(exp(-3*I*Pi/2)+3/2))/sqrt(2)*U[1]); [Re(V),Im(V)]; end; |
Ce sont deux polygones réciproques.

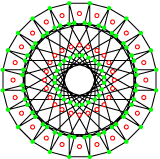
Leur groupe de symétrie est le 4[6]2 d’ordre 92. Le premier possède 48 sommets et 96 arêtes de deux sommets et le second 96 sommets et 48 arêtes de quatre sommets. La projection utilisée ici est
>Trans:=proc(U) local V;
V := expand(U[1]+(exp(I*(-Pi/48))+5/2)/sqrt(3)*U[2]); [Re(V), Im(V)]; end; |
C’est un polygone autodual (égal à son réciproque à une isométrie près).
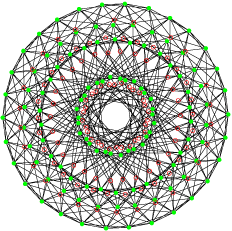
Son groupe de symétrie est le 3[5]3 d’ordre 600. Il possède 120 sommets et 120 arêtes de cinq sommets. La projection utilisée est
>Trans:=proc(U) local a, V;
a := -Pi/25; V := expand(U[1]*(exp(I*a))+(exp(I*(-Pi/25+a))+2)*U[2]); [Re(V), Im(V)]; end; |
Ce sont deux polygones réciproques.

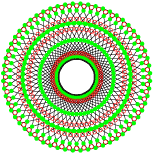
Leur groupe de symétrie est le 3[10]2 d’ordre 720. Le premier possède 240 sommets et 360 arêtes de deux sommets et le second 360 sommets et 240 arêtes de quatre sommets. La projection utilisée ici est
>Trans:=proc(U) local V;
V := expand(U[1]+1.8*U[2]); [Re(V), Im(V)]; end; |
Ce sont deux polygones réciproques.


Leur groupe de symétrie est le 3[10]2 d’ordre 720. Le premier possède 240 sommets et 360 arêtes de deux sommets et le second 360 sommets et 240 arêtes de quatre sommets. La projection utilisée ici est
>Trans:=proc(U) local V;
V := expand(U[1]+1.8*U[2]); [Re(V), Im(V)]; end; |
Certains polygones n’ont pas été encore calculés. En voici la liste:
5{6}2, 2{5}6,5{5}2,2{5}5,2{3}5,5{3}2,3{4}5,5{3}4,3{3}5,5{3}3.
Voici comment calculer les centres des faces d’un polyèdre en Maple sur l’exemple du polyèdre 3{4}2{3}2. Tout d’abord on trouve une face, en calculant l’orbite d’un sommet, qui appartient ni au premier ni au second miroir, par les transformations engendrées par R1 et R2.
>UneFace:={[1,1,1]};
>for i to 10 do UneFace:=UneFace union map(R1,UneFace) union map(R2,UneFace); UneFace:=map(x->map(expand,x),UneFace); print(nops(UneFace)); od: |
On trouve 9 sommets par face. Puis on calcule le centre et l’orbite du centre de cette face.
> LesFaces:={convert(UneFace,`+`)/nops(UneFace)};
>for i to 30 do LesFaces:=LesFaces union map(R1,LesFaces) union map(R2,LesFaces) union map(R3,LesFaces); LesFaces:=map(x->map(expand,x),LesFaces); od: |
On obtient alors 9 faces. Que l’on peut projeter
Faces2D:=evalf(map(Trans,LesFaces)):
|
Là encore, cette dernière variable peut nous permettre de construire un fichier .dat.
Ce sont deux polyèdres réciproques.

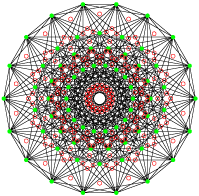
Leur groupe de symétrie est le 3[3]3[4]2 d’ordre 1296. Le premier possède 54 sommets, 216 arêtes de deux sommets et 72 faces de 6 sommets (formant un polygone 2{4}3), le second 72 sommets, 216 arêtes de trois sommets et 54 faces de 8 sommets (formant un polygone 3{3}3). La projection utilisée ici est
>Trans:=proc(U)
o:=arccos(-1/3)/2; a:=Pi; V:=expand(U[1]*exp(I*a)+exp(I*(2*Pi/9+a))*U[2]+exp(I*(4*Pi/9+a))*U[3]); [Re(V),Im(V)]; end; |
Les réflections engendrant le groupe de symétries sont les suivantes
>omega:=exp(2*Pi*I/3);
>R1:=proc(X) map(expand,[omega*X[2],omega^2*X[1],X[3]]);end; >R2:=proc(X) map(expand,[seq(X[i]-I*omega^2/sqrt(3)*(X[1]+X[2]+X[3]),i=1..3)]);end; >R3:=proc(X) map(expand,[X[1],X[2],omega*X[3]]);end; |
C’est un polyèdre autodual (égal à son réciproque à une isométrie près).
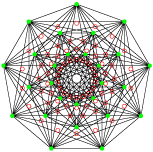
Son groupe de symétrie est le 3[3]3[3]3 d’ordre 648. Il possède 27 sommets, 72 arêtes de 3 sommets et 27 faces de 8 sommets (formant un polygone 3{3}3 . La projection utilisée est
>Trans:=proc(U)
o:=arccos(-1/3)/2; a:=Pi; V:=expand(U[1]*exp(I*a)+exp(I*(2*Pi/9+a))*U[2]+exp(I*(4*Pi/9+a))*U[3]); [Re(V),Im(V)]; end; |
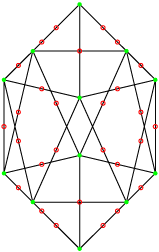
Ce sont deux polyèdres réciproques.
 |  |
Leur groupe de symétrie est le 3[4]2[3]2 d’ordre 162. Le premier possède 9 sommets, 27 arêtes de deux sommets et 27 faces , le second 27 sommets, 27 arêtes de trois sommets et 9 faces. La projection utilisée ici est
>Trans:=proc(U)
dec:=2*Pi/(3*p); V:=expand(U[1]+exp(I*(dec))*U[2]+exp(I*2*dec)*U[3]); [Re(V),Im(V)]; end; |
Ce sont deux polyèdres réels réciproques.
 |  |
Icosaèdre | Dodécaèdre |
Leur groupe de symétrie est le 2[5]2[3]2 d’ordre 120. Le premier possède 12 sommets, 30 arêtes et 20 faces triangulaires , le second 20 sommets, 30 arêtes et 12 faces pentagonales. La projection utilisée ici est simple:
>Trans:=proc(U) [U[1], U[2]-U[3]]; end;
|
C’est un polytope autodual (égal à son réciproque à une isométrie près).

Son groupe de symétrie est le 3[3]3[3]3[3]3 d’ordre 155520. Il possède 240 sommets, 2160 arêtes de 3 sommets et 2160 faces de 8 sommets (formant un polygone 3{3}3 et 240 cellules de 27 sommets (formant un polygone Hessien) . La projection utilisée est
>Trans:=proc(U)
o:=Pi/12; a:=Pi; V:=expand(U[1]*exp(I*a)+(exp(I*(o+a)))*U[2]+exp(I*(Pi/2+a))*U[3]+(exp(I*(-o+a)))*U[4]); [Re(V),Im(V)]; end; |
Ce sont deux polytopes réciproques.

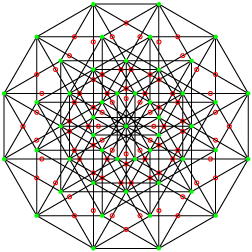
Leur groupe de symétrie est le 3[4]2[3]2[3]2 d’ordre 1944. Le premier possède 12 sommets, 54 arêtes de deux sommets, 324 faces et 729 cellules, le second 729 sommets, 324 arêtes de trois sommets , 54 faces et 12 cellules. La projection utilisée ici est
>Trans:=proc(U)
a:=exp(I*Pi/2); b:=exp(I*Pi/3); c:=exp(I*(Pi/3+Pi/2)); V:=expand(U[1]+a*U[2]+b*U[3]+c*U[4]); [Re(V),Im(V)]; end; |
Ce sont deux polytopes réels réciproques. C’est l’hypercube et son réciproque.
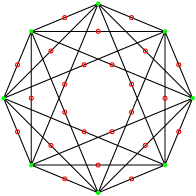 |  |
16-tope | Hypercube |
Leur groupe de symétrie est le 2[4]2[3]2[3]2 d’ordre 1944. Le premier possède 16 sommets, 32 arêtes, 24 faces et 12 cellules, le second 12 sommets, 24 arêtes , 32 faces et 16 cellules. La projection utilisée ici est
>Trans:=proc(U)
u[1]:=0; u[2]:=Pi/2; u[3]:=Pi/4; u[4]:=3*Pi/4; [sum(U[j]*cos(u[j]),j=1..4),sum(U[j]*sin(u[j]),j=1..4)]; end; |
C’est un polytope réel autodual (égal à son réciproque à une isométrie près).
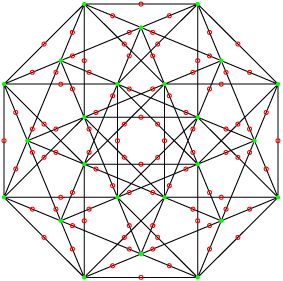
Son groupe de symétrie est le 2[3]2[4]2[3]2 (c’est à dire F4) d’ordre 1152. Il possède 24 sommets, 96 arêtes et 96 faces triangulaires et 24 cellules de 6 sommets . La projection utilisée est
>Trans:=proc(U)
u[1]:=0; u[2]:=Pi/2; u[3]:=Pi/2; u[4]:=Pi; [sum(U[j]*cos(u[j]),j=1..4),sum(U[j]*sin(u[j]),j=1..4)]; end; |
Ce sont deux polytopes réels réciproques. C’est le 600-tope (ou hypericosaedre) et son réciproque le 120-tope.
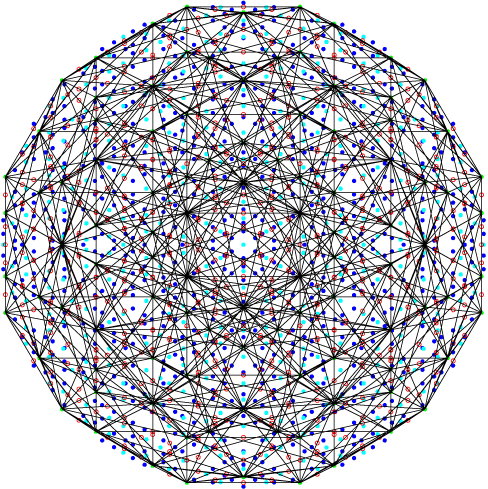 | 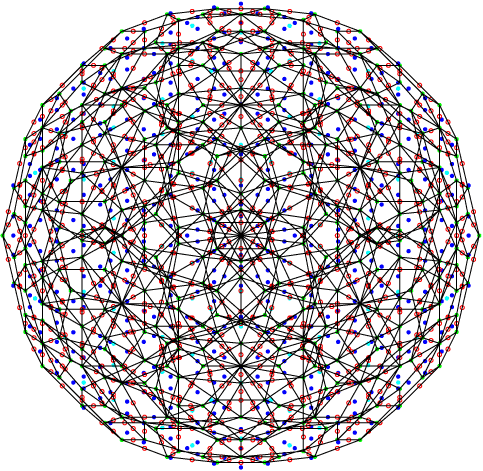 |
600-tope | 120 - tope |
Leur groupe de symétrie est le 2[5]2[3]2[3]2 (c’est à dire H4) d’ordre 14440. Le premier possède 120 sommets, 720 arêtes, 1200 faces triangulaires et 600 cellules icosaedrales, le second 600 sommets, 1200 arêtes , 720 faces pentagonales et 120 cellules dedecaedrales. La projection utilisée ici est
>Trans:=proc(U)
[U[1]+U[3],U[2]+U[4]]; end; |