next up previous
Next: About this document ...

PC 3

Récursivité




Généralités L'utilisation de la récursivité permet d'écrire en général plus facilement les programmes : c'est une traduction directe des définitions par récurrence.

Cependant, les performances (en temps ou en place) des programmes ainsi écrits sont parfois beaucoup moins bonnes.

On peut dans certains cas commencer par écrire en récursif (prototypage) pour optimiser ensuite.

Exemples simples

Calcul de $n!=n\times (n-1)!$ : 

static int fact(int n ) {
  return (n == 0)?  1 : n * fact(n-1);
}

Calcul du pgcd de m et n

static int pgcd (int m, int n) {
  return (m == 0)?  n : pgcd(n % m, m);
}
L'algorithme converge car n+m diminue.

L'écriture en binaire Pour écrire un entier x en binaire, on peut utiiser la formule récursive

bin(x)=(bin(q),r)

avec x=2q+r. On en déduit facilement 
static void binaire(int x) {
  if (x>= 2) binaire(x/2);
  System.out.print(x%2);
}

Suites de Farey On cherche à donner dans l'ordre la suite F(N) des nombres rationnels $0\leq p/q\leq 1$ tels que $p\leq N$. On utilise la classe 

class Rat{
  final static int N=5;
  int num, den;
  Rat(int n, int m) { num= n; den=m; }
  static void Farey(Rat x, Rat y) {
    Rat m= new 
      Rat(x.num+ y.num, x.den + y.den);
    if (m.den <= N) {
      Farey(x,m);
      System.out.print(m.num +"/"+ m.den);
      Farey(m,y);
    }
  }

  public static void main(String[] args) {
    Rat
     zero=new Rat(0,1),
     un= new Rat(1,1);
    Farey(zero,un);
}
La fonction Farey affiche les éléments de F(N) dans ]x,y[pour x=p/q,y=r/s avec qr-ps=1.

Résultat : 

 1/5 1/4 1/3 2/5 1/2 3/5 2/3 3/4 4/5

Comment ça marche? La mémoire est gérée de façon dynamique : une nouvelle zone est utilisée pour chaque appel de la fonction dans la pile d'exécution. De cette façon, les anciennes valeurs ne sont pas écrasées.

Pour chaque appel, on reserve des places dans un enregistrement d'activation pour :

pile183mm170mm600La pile d'execution

Suite de Fibonacci
Suite récurrente linéaire Fn définie par F0=F1=1 et

Fn=Fn-1+Fn-2

On a $F_n\simeq \varphi^n$ avec $\varphi=(1+\sqrt{5})/2$. Calcul récursif: 
static int Fibo(int n) {
 return (n <= 1)? 
    1 : Fibo(n-1)+Fibo(n-2);
}
Temps de calcul:

T(n)=T(n-1)+T(n-2)

d'où

\begin{displaymath}T(n)\simeq F_n\end{displaymath}

Calcul itératif: 

static int Fibo(int n) {
  int i, u, v;
  u = 1; v = 1;
  for (i = 2; i<= n; ++i) {
    v = u + v;
    u = v - u;
  }
  return v;
}
Forme matricielle:

\begin{displaymath}\left[ \begin{array}{c} \par u_n\\ u_{n-1} \end{array}\right... ... \left[ \begin{array}{c} u_{n-1}\\ u_{n-2} \end{array}\right] \end{displaymath}

La fonction d'Ackerman


C'est la fonction définie par: 

static int Ack (int m, int n) {
  if (m  == 0) return n+1;
  else if (n == 0) return Ack(m-1, 1);
  else return Ack (m-1, Ack(m, n-1));
}
Premières valeurs:

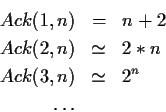
\begin{eqnarray*}Ack(1,n)&=&n+2\\ Ack(2,n)&\simeq&2*n\\ Ack(3,n)&\simeq&2^n\\ \ldots \end{eqnarray*}


Fractales


Principe: objets définis par itération de transformations et donc aisément définissables récursivement.

Un exemple possible est le dragon de Heighway, qui est la courbe obtenue ainsi: dragon162mm139mm600

La courbe du dragon de Heighway est donnée par l'applet suivante: 

import java.awt.*;
import java.applet.*;

public class Dragon extends Applet {

  public void paint(Graphics g) {
    g.setColor(Color.red);
    drawDragon(g, 20, 100, 100, 200, 200);
  }
  void drawDragon (Graphics g, int n,
      int x, int y, int z, int t) {
    int u, v;
    if (n == 1) 
      g.drawLine (z, t);
    else {
      u = (x + z + t - y) / 2;
      v = (y + t - z + x) / 2;
      drawDragon (n - 1, x, y, u, v);
      drawDragon (n - 1, z, t, u, v);
    }
  }
}
Execution d'une applet On crée un fichier Dragon.html contenant 
<HTML>
<HEAD>
<TITLE> Courbe du dragon </TITLE>
</HEAD>

<BODY>
<APPLET CODE="Dragon.class" WIDTH=600
                     HEIGTH=600></APPLET>
</BODY>
</HTML>
on ouvre ensuite ce fichier sous Netscape ou directement par 
appletviewer Dragon.html
Les tours de Hanoi
Problème: On dispose n plaques sur le piquet 1 et on a deux autres piquets vides. On veut amener toutes les plaques du piquet 1 au piquet 3 en respectant les règles suivantes:

1.
Une plaque ne peut être placée que sur une plus grande.
2.
On ne peut déplacer qu'une plaque à la fois.

hanoi106mm44mm700Le cas n=3

Solution récursive: 

static void Hanoi (int n, int i, int j) {
  if (n > 0) {
    Hanoi (n-1, i, 6 - (i+j));
    System.out.print(i+"->"+ j);
    Hanoi (n-1, 6 - (i+j), j);
  }
}

Quicksort
C'est l'une des méthodes de tris les plus efficaces en pratique (tri interne standard d'Unix) avec les caractéristiques suivantes:
1.
Temps $O(n\log n)$ en moyenne (mais pas dans le pire des cas) avec une petite constante.
2.
Tri sur place (espace constant)
Principe: 
void QSort (int g, int d) {
  int i;
  if (g < d) {
    v = a[d];
  {\it partitionner le tableau autour de v}
  {\it et mettre $v$ a sa bonne position $i$}
  QSort (g, i - 1); QSort (i + 1, d);
  }
}
Le programme (version de R. Sedgewick): 
void QSort (int g, int d) { 
  int i, j, t, v;
  if (g < d) {
    v = a[d]; i = g - 1; j = d;
    do {
      do 
        ++i;
      while (a[i] < v);
      do
        --j;
      while (a[j] > v);
      t = a[i]; a[i] = a[j]; a[j] = t;
    } while (j > i);
    a[j] = a[i]; a[i] = a[d]; a[d] = t;
    QSort(g, i - 1);
    QSort(i + 1,d);
  }
}


 
next up previous
Next: About this document ...
Dominique Perrin
1998-12-03