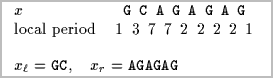The pattern x is factorized in two parts x and xr such that x=x
and xr such that x=x xr. Then the search phase of the Two Way algorithm consists in comparing the characters of xr from left to right and then, if no mismatch occurs during that first stage, in comparing the characters of x
xr. Then the search phase of the Two Way algorithm consists in comparing the characters of xr from left to right and then, if no mismatch occurs during that first stage, in comparing the characters of x from right to left in a second stage.
from right to left in a second stage.
The preprocessing phase of the algorithm consists then in choosing a good factorization x xr.
xr.
Let (u, v) be a factorization of x. A repetition in (u, v) is a word w such that the two following properties hold:
- w is a suffix of u or u is a suffix of w;
- w is a prefix of v of v is a prefix of w.
In other words w occurs at both sides of the cut between u and v with a possible overflow on either side. The length of a repetition in (u,v) is called a local period and the length of the smallest repetition in (u,v) is called the local period and is denoted by r(u,v).
Each factorization (u,v) of has at least one repetition. It can be easily seen that 1  r(u,v)
r(u,v)  |x|
|x|
A factorization (u,v) of x such that r(u,v)=per(x) is called a critical factorization of x.
If (u,v) is a critical factorization of x then at the position |u| in x the global and the local periods are the same. The Two Way algorithm chooses the critical factorization (x ,xr) such that |x
,xr) such that |x | < per(x) and |x
| < per(x) and |x | is minimal.
| is minimal.
To compute the critical factorization x ,xr of x we first compute the maximal suffix z of x for the order
,xr of x we first compute the maximal suffix z of x for the order  and the maximal suffix
and the maximal suffix 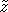 for the reverse order
for the reverse order 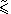 . Then (x
. Then (x ,xr) is chosen such that. |x
,xr) is chosen such that. |x |=max{|z|,|
|=max{|z|,|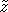 |}
|}
The preprocessing phase can be done in O(m) time and constant space complexity.
The searching phase of the Two Way algorithm consists in first comparing the character of xr from left to right, then the character of x from right to left.
from right to left.
When a mismatch occurs when scanning the k-th character of xr, then a shift of length k is performed.
When a mismatch occurs when scanning x , or when an occurrence of the pattern is found, then a shift of length per(x) is performed.
, or when an occurrence of the pattern is found, then a shift of length per(x) is performed.
Such a scheme leads to a quadratic worst case algorithm, this can be avoided by a prefix memorization: when a shift of length per(x) is performed the length of the matching prefix of the pattern at the beginning of the window (namely m-per(x)) after the shift is memorized to avoid to scan it again during the next attempt.
The searching phase of the Two Way algorithm can be done in O(n) time complexity.
The Two Way algorithm performs 2n-m text character comparisons in the worst case. Breslauer designed a variation on the Two Way algorithm which performs less than 2n-m comparisons using constant space.