 be a ring of coefficients and
be a ring of coefficients and 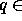 . The usual Hecke
algebra of type A
(
. The usual Hecke
algebra of type A
(HEQA ),
denoted 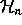 is a deformation of the symmetric
group algebra. With
is a deformation of the symmetric
group algebra. With 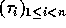 as set of generators, its
presentation is
as set of generators, its
presentation is



Let  be a ring of coefficients and
be a ring of coefficients and 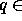 . The usual Hecke
algebra of type A
(
. The usual Hecke
algebra of type A
(HEQA ),
denoted 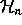 is a deformation of the symmetric
group algebra. With
is a deformation of the symmetric
group algebra. With 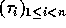 as set of generators, its
presentation is
as set of generators, its
presentation is
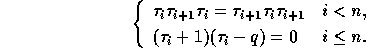
As the braid relations appear in the presentation, the product
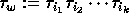 is independent of the reduced
decomposition
is independent of the reduced
decomposition 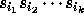 of the
permutation w. It is well known that
of the
permutation w. It is well known that 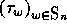 is a
linear basis of the free module
is a
linear basis of the free module 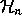 . Hence, for n<m, we get a
natural embedding
. Hence, for n<m, we get a
natural embedding 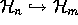 , and define
, and define

The typical element of 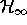 then is the sum
then is the sum
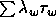 .
There is a unique scalar product
(
.
There is a unique scalar product
(HeqaScal )
on 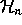 satisfying
satisfying
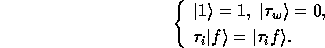
It will be called invariant
and, if  is a field and q not a root
of unity, it makes
is a field and q not a root
of unity, it makes 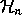 into a symmetric algebra.
into a symmetric algebra.
Remarkable self-adjoint elements are the Jucis-Murphy ones
(HeqaJucis ). They are
the q-deformation of the elements previously defined for the symmetric
group. The k-th (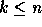 ) Jucis-Murphy element is equal to
) Jucis-Murphy element is equal to

In case 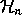 is semi-simple, they generate a (self-adjoint) maximal
commutative subalgebra. Minimal idempotents are polynomials in these elements
(polynôme gallois
computed by the
is semi-simple, they generate a (self-adjoint) maximal
commutative subalgebra. Minimal idempotents are polynomials in these elements
(polynôme gallois
computed by the HeqaGall function )
indexed by tableaux.
We can construct a complete family of irreducible representations
(HeqaRepT and
HeqaRepCT )
as orbits
of q-deformation of the Vandermonde determinant. For an integral vector
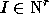 , let
, let 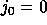 ,
, 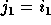 ,
, 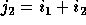 ,
,  ,
,
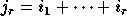 . The q-Vandermonde of index I is by definition
. The q-Vandermonde of index I is by definition
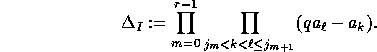
The deformation of the usual Specht modules is then provided by the
orbit of 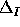 under an action on polynomials which is the quotient
of the faithful representation of
under an action on polynomials which is the quotient
of the faithful representation of 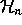 as divided difference operators
[] that is, for h<k,
as divided difference operators
[] that is, for h<k,
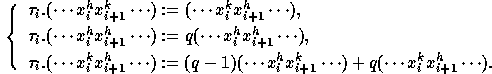
When I is increasing (resp. decreasing) a natural basis
of the Specht module is indexed by contretableaux (resp. tableaux).
In the semi-simple case, inverses in 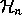 can be computed by means of
the minimal polynomials
(
can be computed by means of
the minimal polynomials
(HeqaMinT and
HeqaMinCT ).
For 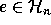 , I an integral vector
(a shape) and x an indeterminate, let
, I an integral vector
(a shape) and x an indeterminate, let 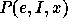 denote the minimal
polynomial for the matrix of e in a representation of shape I. The
minimal polynomial Q of e in
denote the minimal
polynomial for the matrix of e in a representation of shape I. The
minimal polynomial Q of e in 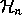 is then
is then
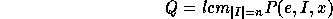
which can be written 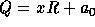 . If
. If 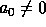 , we get
, we get
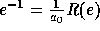 (these elements being computed by the use of the
(these elements being computed by the use of the
HeqaInv function ).


