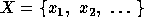 an infinite set of commutative
indeterminates, which will be called an alphabet. The
elementary symmetric functions
an infinite set of commutative
indeterminates, which will be called an alphabet. The
elementary symmetric functions 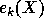 are defined by
the generating series
are defined by
the generating series



The basic reference for this section is Macdonald's book [].
Let 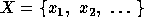 an infinite set of commutative
indeterminates, which will be called an alphabet. The
elementary symmetric functions
an infinite set of commutative
indeterminates, which will be called an alphabet. The
elementary symmetric functions 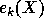 are defined by
the generating series
are defined by
the generating series
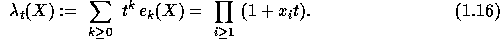
The complete homogeneous symmetric functions 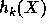 are defined by
are defined by
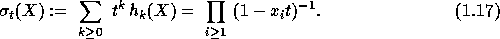
The power sums symmetric functions 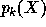 are defined by
are defined by
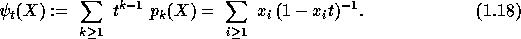
These generating series satisfy the following relations
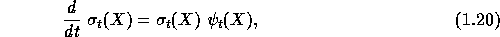
Formula (1.21) is known as Newton's formula. The so-called
fundamental theorem of the theory of symmetric functions states that the
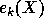 are algebraically independent. Therefore, any formal power
series
are algebraically independent. Therefore, any formal power
series 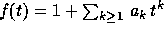 may be considered as the
specialization of the series
may be considered as the
specialization of the series
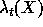 to a virtual set of arguments A.
to a virtual set of arguments A.
We denote by 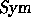 the algebra of symmetric functions, i.e. the
algebra generated over
the algebra of symmetric functions, i.e. the
algebra generated over 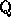 by the elementary functions. It is a graded
algebra for the weight function
by the elementary functions. It is a graded
algebra for the weight function 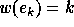 , and the dimension of its
homogeneous component of weight n, denoted by
, and the dimension of its
homogeneous component of weight n, denoted by 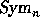 , is equal to
, is equal to 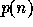 ,
the number of partitions of n. A partition is a
finite non-increasing sequence of positive integers,
,
the number of partitions of n. A partition is a
finite non-increasing sequence of positive integers,
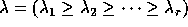 .
We shall also write
.
We shall also write
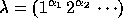 ,
, 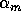 being the
number of parts
being the
number of parts 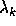 which
are equal to m. The weight of
which
are equal to m. The weight of 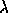 is
is 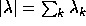 and its length is the
number of its (nonzero) parts
and its length is the
number of its (nonzero) parts 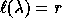 .
.
For a partition 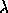 , one sets
, one sets
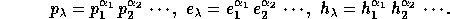
These are linear bases of 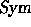 (
(Top ,
Toe ,
Toh ).
For 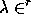 , not necessarily a partition,
the Schur function
, not necessarily a partition,
the Schur function 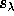 is defined by
is defined by
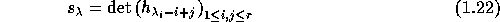
where 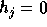 for j<0. The Schur functions indexed by partitions form a
for j<0. The Schur functions indexed by partitions form a
 -basis of
-basis of 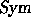 (
(Tos ),
and one usually endows 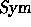 with a scalar product
with a scalar product 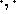 for which this basis is orthonormal. The
for which this basis is orthonormal. The 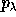 form then an orthogonal
form then an orthogonal
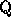 -basis of
-basis of 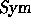 ,
with
,
with 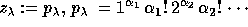 (
(Zee ,
ScalarSf ).
Thus, for a
partition 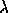 of weigth n,
of weigth n, 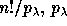 is
the cardinality of the
conjugacy class of
is
the cardinality of the
conjugacy class of 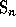 whose elements have
whose elements have 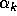 cycles of length k for all
cycles of length k for all 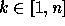 . A permutation
. A permutation  in this
class will be said of type
in this
class will be said of type 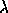 (
(Perm2Cycle ,
Perm2CycleType ),
and we shall write 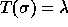 .
.
These definitions are motivated by the following classical results
of Frobenius. Let 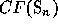 be the ring of central functions
of the symmetric group
be the ring of central functions
of the symmetric group 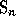 . The Frobenius characteristic map
. The Frobenius characteristic map
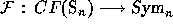 associates (
associates (Sf2Char )
with any central function 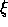 the symmetric function
the symmetric function
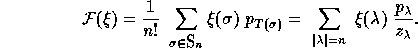
where 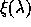 is the common value of the
is the common value of the 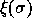 for all
for all  such that
such that 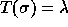 . We can also consider
. We can also consider 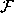 as a map from
the representation ring
as a map from
the representation ring 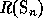 to
to 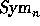 by setting
by setting
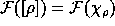 , where
, where 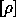 denotes
the equivalence class of a representation
denotes
the equivalence class of a representation 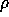 .
Glueing these maps together, one has a linear
map
.
Glueing these maps together, one has a linear
map
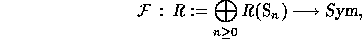
which turns out to be an isomorphism of graded rings.
We denote by 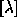 the class of the irreducible
representation of
the class of the irreducible
representation of 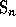 associated with the partition
associated with the partition 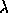 , and by
, and by
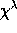 its character. We have then
its character. We have then 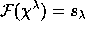 .
.
The product  , defined on the homogeneous component
, defined on the homogeneous component 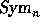 by
by
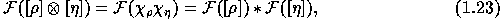
and extended to 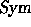 by defining the product of two homogeneous functions
of different weights to be zero, is called the internal product
(
by defining the product of two homogeneous functions
of different weights to be zero, is called the internal product
(ITensor ).
One can identify the tensor product 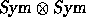 with the algebra
with the algebra
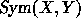 of polynomials which are separately symmetric in two infinite
disjoint sets of indeterminates X and Y, the correspondence
being given by
of polynomials which are separately symmetric in two infinite
disjoint sets of indeterminates X and Y, the correspondence
being given by 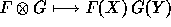 . Denoting by X+Y
the disjoint union of X and Y, one can then define a comultiplication
. Denoting by X+Y
the disjoint union of X and Y, one can then define a comultiplication
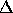 on
on 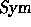 by setting
by setting 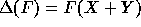 . This comultiplication
endows
. This comultiplication
endows  with the structure of a self-dual Hopf algebra, which is very
useful for calculations involving characters of symmetric groups.
The
basic formulas are
with the structure of a self-dual Hopf algebra, which is very
useful for calculations involving characters of symmetric groups.
The
basic formulas are
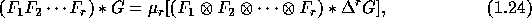
where 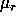 denotes the r-fold ordinary multiplication and
denotes the r-fold ordinary multiplication and
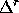 the iterated coproduct, and
the iterated coproduct, and
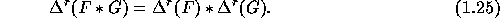
The symmetric functions of the virtual alphabet 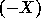 are defined by the generating series
are defined by the generating series
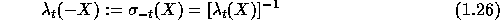
and one can more generally consider differences of alphabets. The symmetric functions of X-Y are given by the generating series
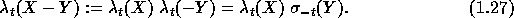
In particular, 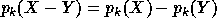 .
.
There is another coproduct 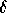 on
on 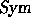 , which is obtained by considering
products instead of sums, that is
, which is obtained by considering
products instead of sums, that is

One can check that its adjoint is the internal product:
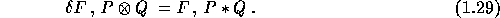
This equation can be used to give an intrinsic definition of the internal
product, i.e. without any reference to characters of the
symmetric group. Also, one can see that two bases 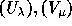 of
of 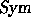 are adjoint to each other iff
are adjoint to each other iff
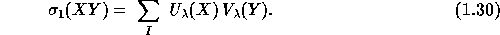
For example, writing 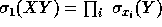 and expanding
the product, one obtains that the adjoint basis of
and expanding
the product, one obtains that the adjoint basis of 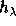 is formed by the
monomial functions
is formed by the
monomial functions 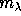 .
.


