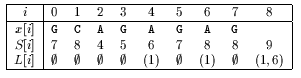Next: Galil-Seiferas algorithm Up: ESMAJ Prev: BNDM algorithm
- version of the Reverse Factor algorithm using the suffix oracle of xR instead of the suffix automaton of xR;
- fast in practice for very long patterns and small alphabets;
- preprocessing phase in O(m) time and space complexity;
- searching phase in O(mn) time complexity;
- optimal in the average.
The Boyer-Moore type algorithms match some suffixes of the pattern but it is possible to match some prefixes of the pattern by scanning the character of the window from right to left and then improve the length of the shifts. This is make possible by the use of the suffix oracle of the reverse pattern. This data structure is a very compact automaton which recognizes at least all the suffixes of a word and slightly more other words The string-matching algorithm using the oracle of the reverse pattern is called the Backward Oracle Matching algorithm.
The suffix oracle of a word w is a Deterministic Finite Automaton O(w) =(Q, q0, T, E).
The language accepted by O(w) is such that {u in  * : exists v in
* : exists v in  * such that w = vu} in L(O(w)).
* such that w = vu} in L(O(w)).
The preprocessing phase of the Backward Oracle Matching algorithm consists in computing the suffix oracle for the reverse pattern xR. Despite the fact that it is able to recognize words that are not factor of the pattern, the suffix oracle can be used to do string-matching since the only word of length greater or equal m which is recognized by the oracle is the reverse pattern itself. The computation of the oracle is linear in time and space in the length of the pattern.
During the searching phase the Backward Oracle Matching algorithm parses the characters of the window from right to left with the automaton O(xR) starting with state q0. It goes until there is no more transition defined for the current character. At this moment the length of the longest prefix of the pattern which is a suffix of the scanned part of the text is less than the length of the path taken in O(xR) from the start state q0 and the last final state encountered. Knowing this length, it is trivial to compute the length of the shift to perform.
The Backward Oracle Matching algorithm has a quadratic worst case time complexity but it is optimal in average. On the average it performs O(n.(log m) / m) inspections of text characters reaching the best bound shown by Yao in 1979.
m) / m) inspections of text characters reaching the best bound shown by Yao in 1979.
Only the external transitions of the oracle are stored in link lists (one per state). The labels of these transitions and all the other transitions are not stored but computed from the word x. The description of a linked list List can be found in the introduction section implementation.
#define FALSE 0
#define TRUE 1
int getTransition(char *x, int p, List L[], char c) {
List cell;
if (p > 0 && x[p - 1] == c)
return(p - 1);
else {
cell = L[p];
while (cell != NULL)
if (x[cell->element] == c)
return(cell->element);
else
cell = cell->next;
return(UNDEFINED);
}
}
void setTransition(int p, int q, List L[]) {
List cell;
cell = (List)malloc(sizeof(struct _cell));
if (cell == NULL)
error("BOM/setTransition");
cell->element = q;
cell->next = L[p];
L[p] = cell;
}
void oracle(char *x, int m, char T[], List L[]) {
int i, p, q;
int S[XSIZE + 1];
char c;
S[m] = m + 1;
for (i = m; i > 0; --i) {
c = x[i - 1];
p = S[i];
while (p <= m &&
(q = getTransition(x, p, L, c)) ==
UNDEFINED) {
setTransition(p, i - 1, L);
p = S[p];
}
S[i - 1] = (p == m + 1 ? m : q);
}
p = 0;
while (p <= m) {
T[p] = TRUE;
p = S[p];
}
}
void BOM(char *x, int m, char *y, int n) {
char T[XSIZE + 1];
List L[XSIZE + 1];
int i, j, p, period, q, shift;
/* Preprocessing */
memset(L, NULL, (m + 1)*sizeof(List));
memset(T, FALSE, (m + 1)*sizeof(char));
oracle(x, m, T, L);
/* Searching */
j = 0;
while (j <= n - m) {
i = m - 1;
p = m;
shift = m;
while (i + j >= 0 &&
(q = getTransition(x, p, L, y[i + j])) !=
UNDEFINED) {
p = q;
if (T[p] == TRUE) {
period = shift;
shift = i;
}
--i;
}
if (i < 0) {
OUTPUT(j);
shift = period;
}
j += shift;
}
}
The test i + j >= 0 in the inner loop of the searching phase of the function BOM is only necessary during the first attempt if x occurs at position 0 on y. Thus to avoid testing at all the following attempts the first attempt could be distinguished from all the others.
Preprocessing phase

Oracle used by Backward Oracle Matching algorithm.
Searching phase
- ALLAUZEN C., CROCHEMORE M., RAFFINOT M., 1999, Factor oracle: a new structure for pattern matching, in Proceedings of SOFSEM'99, Theory and Practice of Informatics, J. Pavelka, G. Tel and M. Bartosek ed., Milovy, Czech Republic, Lecture Notes in Computer Science 1725, pp 291-306, Springer-Verlag, Berlin.




Next: Galil-Seiferas algorithm Up: ESMAJ Prev: BNDM algorithm
 * : exists v in
* : exists v in  * such that w = vu} in L(O(w)).
* such that w = vu} in L(O(w)). m) / m) inspections of text characters reaching the best bound shown by Yao in 1979.
m) / m) inspections of text characters reaching the best bound shown by Yao in 1979.