Throughout this section we will use a constant k. Galil and Seiferas suggest that practically this constant could be equal to 4.
Let us define the function reach for 0  i < m as follows: reach(i)=i+max{i’
i < m as follows: reach(i)=i+max{i’  m-i : x[0 .. i’]=x[i+1 .. i’+i+1]}
m-i : x[0 .. i’]=x[i+1 .. i’+i+1]}
Then a prefix x[0 .. p] of x is a prefix period if it is basic and reach(p)  kp.
kp.
The preprocessing phase of the Galil-Seiferas algorithm consists in finding a decomposition uv of x such that v has at most one prefix period and |u|=O(per(v)). Such a decomposition is called a perfect factorization.
Then the searching phase consists in scanning the text y for every occurrences of v and when v occurs to check naively if u occurs just before in y.
In the implementation below the aim of the preprocessing phase (functions newP1, newP2 and parse) is to find a perfect factorization uv of x where u=x[0 .. s-1] and v=x[s .. m-1]. Function newP1 finds the shortest prefix period ofx[s .. m-1]. Function newP2 finds the second shortest prefix period of x[s .. m-1] and function parse increments s.
- Before calling function search we have:
-

x[s .. m-1] has at most one prefix period; -

if x[s .. m-1] does have a prefix period, then its length is p1; -

x[s .. s+p1+q1-1] has shortest period of length p1; -

x[s .. s+p1+q1] does not have period of length p1.
The pattern x is of the form x[0 .. s-1]x[s .. m-1] where x[s .. m-1] is of the form z z’az” with z basic, |z|=p1, z’ prefix of z, z’a not a prefix of z and |z
z’az” with z basic, |z|=p1, z’ prefix of z, z’a not a prefix of z and |z z’| =p1+q1 (see figure 24.1).
z’| =p1+q1 (see figure 24.1).
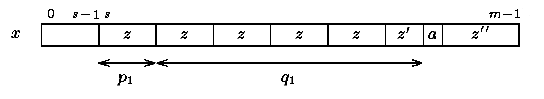
Figure 24.1: A perfect factorization of x.
- It means that when searching for x[s .. m-1] in y:
-

if x[s .. s+p1+q1-1] has been matched a shift of length p1 can be performed and the comparisons are resumed with x[s+q1]; -

otherwise if a mismatch occurs with x[s+q] with q  p1+q1 then a shift of length q/k+1 can be performed and the comparisons are resumed with x[0].
p1+q1 then a shift of length q/k+1 can be performed and the comparisons are resumed with x[0].
This gives an overall linear number of text character comparisons.
The preprocessing phase of the Galil-Seiferas algorithm is in O(m) time and constant space complexity. The searching phase is in O(n) time complexity. At most 5n text character comparisons can be done during this phase.



