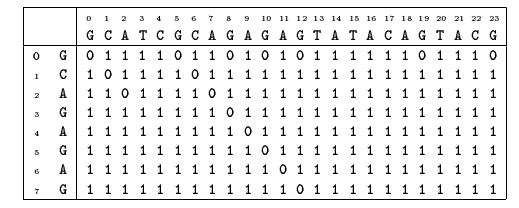
The Shift Or algorithm uses bitwise techniques. Let R be a bit array of size m. Vector Rj is the value of the array R after text character y[j] has been processed (see figure 5.1). It contains informations about all matches of prefixes of x that end at position j in the text for 0 < i  m-1:
m-1:

Figure 5.1: Meaning of vector Rj.
The vector Rj+1 can be computed after Rj as follows. For each Rj[i]=0:
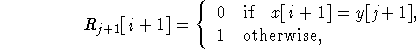
and
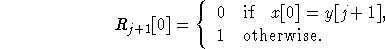
If Rj+1[m-1]=0 then a complete match can be reported.
The transition from Rj to Rj+1 can be computed very fast as follows: For each c in  , let Sc be a bit array of size m such that: for 0
, let Sc be a bit array of size m such that: for 0  i < m-1, Sc[i]=0 iff x[i]=c.
i < m-1, Sc[i]=0 iff x[i]=c.
The array Sc denotes the positions of the character c in the pattern x. Each Sc can be preprocessed before the search. And the computation of Rj+1 reduces to two operations, shift and or: Rj+1=SHIFT(Rj) OR Sy[j+1]
Assuming that the pattern length is no longer than the memory-word size of the machine, the space and time complexity of the preprocessing phase is O(m+ ).
).
The time complexity of the searching phase is O(n), thus independent from the alphabet size and the pattern length.
int preSo(char *x, int m, unsigned int S[]) {
unsigned int j, lim;
int i;
for (i = 0; i < ASIZE; ++i)
S[i] = ~0;
for (lim = i = 0, j = 1; i < m; ++i, j <<= 1) {
S[x[i]] &= ~j;
lim |= j;
}
lim = ~(lim>>1);
return(lim);
}
void SO(char *x, int m, char *y, int n) {
unsigned int lim, state;
unsigned int S[ASIZE];
int j;
if (m > WORD)
error("SO: Use pattern size <= word size");
/* Preprocessing */
lim = preSo(x, m, S);
/* Searching */
for (state = ~0, j = 0; j < n; ++j) {
state = (state<<1) | S[y[j]];
if (state < lim)
OUTPUT(j - m + 1);
}
}
 ) time and space complexity;
) time and space complexity;



 m-1:
m-1:
 , let Sc be a bit array of size m such that: for 0
, let Sc be a bit array of size m such that: for 0