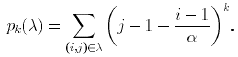Jack polynomials and alpha-contents
Page of Michel Lassalle
List of publications
Some preprints
Tables for
characters of the
symmetric group
Symmetric functions
and
Jucys-Murphy elements
Tables for
Jack polynomials :
A conjecture for
Jack polynomials
Jack polynomials
and free cumulants
This page gives new data for Jack polynomials.Being given some parameter &alpha and an arbitrary partition &lambda, we consider the Jack polynomial associated to &lambda, and its development in terms of the power sum symmetric functions, i.e. we write
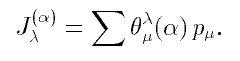
We give the explicit expression of the coefficients &theta (&lambda,&mu) appearing in this development, in terms of the &alpha-contents of &lambda.
We list these coefficients for any partition &mu, such that weight(&mu) - length(&mu) < 11.
Thanks are due to Alain Lascoux for implementing our method on computer, using ACE.
Tables giving &theta (&lambda,&mu) for weight(&mu) - length(&mu)Tables for bigger values may be given upon request.
For &alpha = 1 ( i.e. a = 1 and b = 0 ), these tables give the central characters of the symmetric group.
Our results are in Maple format. They should be read as follows.Example :
- The parameter &alpha is denoted by the letter a, and the letter b stands for (&alpha - 1).
- The partition &lambda is kept arbitrary.
The letter W stands for the weight of &lambda, and p_k (k > 0) stands for the k-th power sum of the &alpha-contents of &lambda, i.e.
- &mu denotes a partition without any part 1.
- Each table gives first the partition &mu, then
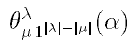
[2]
a*p1
[3]
-a*b*p1+a^2*p2+a*(1/2*W-1/2*W^2)
means
Last modified : May 16, 2004
Back to top