
Symmetric functions and Jucys-Murphy elements
Page of Michel Lassalle
List of publications
Some preprints
Tables for
characters of the
symmetric group
Tables for
Jack polynomials :
Jack polynomials
and alpha-contents
A conjecture for
Jack polynomials
Jack polynomials
and free cumulants
This page gives new data for the class expansion of the Hall-Littlewood polynomial taken at the Jucys-Murphy elements of the symmetric group. Our results have been published there.We consider the Hall-Littlewood polynomial Pk(x1,x2,...,xn;z), its specialization at the Jucys-Murphy elements J1,J2,...,Jn of the symmetric group of n letters, and the development of this specialization in terms of the Farahat-Higman classes, i.e. we write
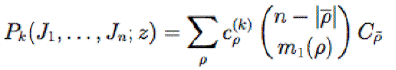
We give the generating functions of the coefficients, i.e.
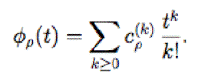
For z = 0 ( respectively z = 1 ), our tables correspond to the case of complete symmetric functions hk (respectively power sums pk).
Tables giving the function &Phi&rho(t) for weight of &rho from 3 to 14Tables for bigger values may be given upon request.
Our results are in Maple format. They should be read as follows.
- The letter z stands for the parameter of the Hall-Littlewood polynomial.
- The letter q stands for exp(t).
- The table gives first the partition &rho, then &Phi&rho(t).
Example :
[3]
-1/3*q+1/3*q^2+1/6/q*z+1/6*q*z-1/6/q^2*z-1/3/q+1/3/q^2-1/6*q^2*z
Last modified : May 8, 2010
Back to top