Border Table

The border table or good prefix table of a non-empty word $x$ is defined on the lengths $\ell$, $\ell=0, \dots, |x|$, of its prefixes both by $border[0] = -1$ and, for $\ell\gt 0$, by $border[\ell] = |Border(x[0..\ell-1])|$. Here is the border table of the word abaababaaba:
$i$ 012345678910
$x[i]$ abaababaaba
$\ell$ 01234567891011
$border[\ell]$ -100112323456

It can be computed in $O(|x|)$ time by the following algorithm.

Borders$(x \mbox{ non-empty word of length } m)$ 
    \begin{algorithmic}
\STATE $border[0]\leftarrow -1$
\STATE $i\leftarrow 0$
\FOR{$j\leftarrow 1$ \TO $m-1$}
    \STATE $border[j]\leftarrow i$
    \WHILE{$i\geq 0$ \AND $x[i]\neq x[j]$}
        \STATE $i\leftarrow border[i]$
    \ENDWHILE
    \STATE $i\leftarrow i+1$
\ENDFOR
\STATE $border[m]\leftarrow i$
\RETURN $border$
    \end{algorithmic}

Example

Let us consider the prefix $u=$abaababa of the above word. Its border is $v=$aba of length $3=border[8]$. The next letter a extends the border, that is, $Border(u$a$) = v$a.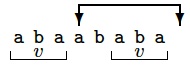
Border Table
If the next letter $c$ is not a, the border of $uc$ is the border of $vc$, which sketches the proof of the recurrence relation, for $u$ a word and $c$ a letter: $$ Border(uc)=\cases{ Border(u)c & if $Border(u)c$ is a prefix of $u$, \cr Border(Border(u)c) & otherwise. \cr } $$

The border table is used in the Morris-Pratt (MP) exact string matching algorithm.

References

  • M. Crochemore, C. Hancart, and T. Lecroq. Algorithms on Strings. Cambridge University Press, 2007. 392 pages.
  • M. Crochemore, T. Lecroq, and W. Rytter. 125 Problems in Text Algorithms. Cambridge University Press, 2021.
  • M. Crochemore and W. Rytter. Text algorithms. Oxford University Press, 1994. 412 pages.
  • D. Gusfield. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. Cambridge University Press, Cambridge, 1997.
  • G. Navarro and M. Raffinot. Flexible pattern matching in strings - practical on-line search algorithms for texts and biological sequences. Cambridge University Press, 2002.
  • B. Smyth. Computing Patterns in Strings. Pearson Education Limited, Harlow, England, 2003. 423 pages.