Subsequence Automaton

\( \def\sa#1{\tt{#1}} \def\dd{\dot{}\dot{}} \def\aSMot{\mathcal{SM}} \)

Subsequences (or subwords) occurring in a word are useful elements to filter series of texts or to compare them. The basic data structure for developing applications related to subsequences is an automaton accepting them due to its reasonable size.

For a non-empty word $y$, let $\aSMot(y)$ be the minimal (deterministic) automaton accepting the subsequences of $y$. It is also called the Deterministic Acyclic Subsequence Graph (DASG). Below is the subsequence automaton of $\sa{abcabba}$. All its states are terminal and it accepts the set $$\{\sa{a},\sa{b},\sa{c},\sa{aa},\sa{ab},\sa{ac}, \sa{ba},\sa{bb},\sa{bc},\sa{ca},\sa{cb},\sa{aaa}, \sa{aab},\sa{aba},\sa{abb},\sa{abc},\dots\}.$$

DASG

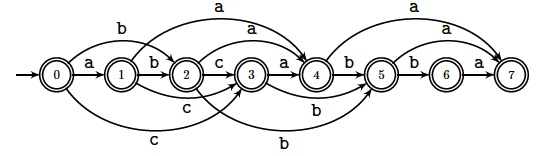
Subsequence automata are an essential structure to find words that discriminate two words because they provide a direct access to all their subsequences. A word $u$ distinguishes two distinct words $y$ and $z$ if it is a subsequence of only one of them, that is, if it is in the symmetric difference of their associated sets of subsequences.

The subsequence automaton of a word $y$ of length $n$ on an alphabet $A$ can be computed in time $O(n\times |A|)$ by the following algorithm.
DASG$(y \textrm{ non-empty word of length }n)$ 
    \begin{algorithmic}
\FOR{each letter $a \in alph(y)$}
  \STATE{$t[a]\leftarrow 0$}
\ENDFOR
\FOR{$i\leftarrow 0$ \TO $n-1$}
  \FOR{$j\leftarrow t[y[i]]$ \TO $i$}
    \STATE{$goto(j,y[i])\leftarrow i+1$}
  \ENDFOR 
  \STATE{$t[y[i]]\leftarrow i+1$}
\ENDFOR
    \end{algorithmic}

References

  • A. V. Aho, J. E. Hopcroft, and J. D. Ullman. The Design and Analysis of Computer Algorithms. Addison-Wesley, 1974.
  • R. A. Baeza-Yates. Searching subsequences. Theor. Comput. Sci., 78(2):363-376, 1991.
  • T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein. Introduction to Algorithms, 3rd Edition. MIT Press, 2009.
  • M. Crochemore, T. Lecroq, and W. Rytter. 125 Problems in Text Algorithms. Cambridge University Press, 2021.
  • M. Crochemore and Z. Tronicek. On the size of DASG for multiple texts. In A. H. F. Laender and A. L. Oliveira, editors, String Processing and Information Retrieval, 9th International Symposium, SPIRE 2002, Lisbon, Portugal, September 11-13, 2002, Proceedings, volume 2476 of Lecture Notes in Computer Science, pages 58-64. Springer, 2002.
  • Z. Tronicek and B. Melichar. Directed acyclic subsequence graph. In J. Holub and M. Simánek, editors, Proceedings of the Prague Stringology Club Workshop 1998, Prague, Czech Republic, September 3-4, 1998, pages 107-118. Department of Computer Science and Engineering, Faculty of Electrical Engineering, Czech Technical University, 1998.
  • Z. Tronicek and A. Shinohara. The size of subsequence automaton. Theor. Comput. Sci., 341(1-3):379-384, 2005.