OpenGL
Les transformations
Les transformations dans OpenGL
En mathématique, une transformation géométrique est une fonction qui associe un ensemble de valeurs à un autre ensemble ou à soit même. D'un point de vue d'un plan, d'un schéma ou d'une scène, une transformation géométrique permet de "déplacer" un ensemble de points et de sommets par rotation, symétrie, ou translation. Il est dit qu'une transformation est un changement de repère.
La transformation est une notion complexe mais très importante pour les bibliothèques graphiques. Nous pouvons modifier un objet (ou un vecteur) dans un plan ou le transposer dans un espace grâce aux transformations.
Sous OpenGL, les transformations sont caractérisées par des matrices et des calculs matriciels.
Pour représenter la caméra (et la scène), l'API possède au moins 4 piles de matrices différentes :
- Pour la projection: Pour ajuster la perspective de la scène (dont le champ de vision et le zoom)
- Pour la vue: Pour positionner et orienter la vue de la scène.
- Pour le modèle: Pour déplacer les objets dans la scène.
- Pour le "viewport": Pour agir sur des images en 2D (dont leurs tailles).
Nous parlons de "pile" de matrices, car il est possible de stocker et de déstocker une matrice dans une pile (pour sauvegarder et charger un repère).
Une transformation d'un plan, d'un objet, ou d'un vecteur se résulte par une multiplication de matrices.
Les matrices dans OpenGL
Chaque matrice possède 4 coordonnées. Les piles de matrices qui sont conçu pour les transformations géométriques utilisent ces 4 coordonnées pour représenter les 3 dimensions d'une scène :
 |
|
Il existe bien d'autres matrices dans OpenGL afin de gérer d'autres aspects d'une scène: Par exemple, il existe une matrice de couleurs (coordonnées R, G, B, A) et une matrice de texture (S, T, R, Q).
A partir de ces premières matrices, nous pouvons appliquer les principales transformations, dont la translation, le changement
d'échelle, et la rotation.
Le format des images est la suivante:
[La matrice générée par les paramètres de la fonction] X [La matrice courante] = [La matrice résultat de la fonction]
| La matrice d'identité | |
|---|---|
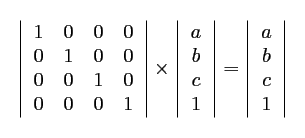 |
Fonction : glLoadIdentity() C'est la matrice "par défaut", qui nous permet de réinitialiser la matrice sous un état et un repère connu. |
| La translation | |
|---|---|
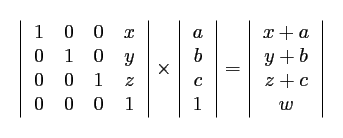 |
Fonction : glTranslate() Le calcul matriciel le plus simple: Nous additionnons chaque dimension avec les paramètres de la méthode. L'objectif de cette fonction est de translater le repère (ou le plan). |
| Le changement d'échelle | |
|---|---|
 |
Fonction : glScale() Le changement d'échelle consiste d'agrandir ou de réduire (zoomer ou de dé-zoomer) un repère. C'est aussi utilisé pour modifier la taille des entités géométriques. |
| La rotation | |
|---|---|
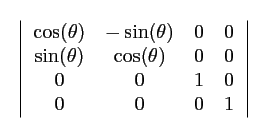 |
Fonction : glRotate() Cette transformation est plus compliqué. L'image sur la gauche représente la formule utilisée pour la rotation sur l'axe Z (en degré). La formule est différente selon la ou les rotations que nous souhaitons appliquer sur le repère. |
Toutes ces transformations sont des multiplications de matrices. Elles appellent la méthode glMultMatrix() afin
de multiplier ces matrices.
Enfin, il est possible d'enregistrer les matrices dans la pile, pour enregistrer les repères avant de la modifier:
glPushMatrix() pour stocker une matrice dans la pile,
et glPopMatrix() pour déstocker et charger la matrice (la plus haute de la pile).
Les piles de matrices de projection et de modèle
Les deux piles de matrices les plus importantes d'OpenGL sont la projection (GL_PROJECTION) et le modèle (GL_MODELVIEW).
La méthode glMatrixMode() permet de changer la pile de matrices courante.
La pile de matrice de projection
Le rôle d'une matrice de projection est de définir la perspective d'un plan, la façon dont sera projeté une scène, du point de vue de la caméra.
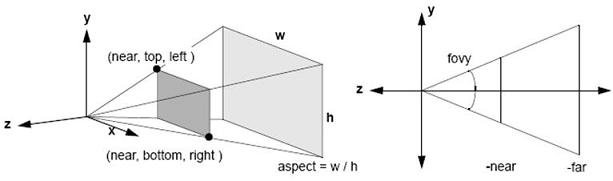 |
Pour réaliser la perspective d'une scène, il existe deux méthodes: GLU.gluPerspective() et glFrustum().
glFrustum() est dédiée pour la projection en perspective.
C'est une méthode complexe: Elle prend plusieurs paramètres (au nombre de 6) qui nécessitent d'être déterminé et calculé avant l'invocation
de la fonction.
Heureusement, la bibliothèque GLU nous offre une méthode plus simple que glFrustum(): GLU.gluPerspective().
La méthode se charge de calculer elle-même la perspective (contrairement à glFrustum()) et nécessite que 4 paramètres :
- fovy: La valeur du champ de vision en degré, sur l'axe Y.
- aspect: "L'aspect ratio", ou le rapport entre la longueur et la largeur de l'écran (ou de la résolution). Ce rapport permet de déterminer le champ de vision sur l'axe X.
- zNear / zFar: Ces deux paramètres sont les limites en profondeur de la perspective.
Pour la projection orthographique, OpenGL possède la fonction glOrtho(). C'est une fonction qui modifie la matrice courante en une matrice orthographique. Ces matrices sont peu utilisés en 3D, mais est adapté pour la rendu en 2D. Comme pour glFrustum(), la méthode nécessite 6 paramètres qui sont simple à obtenir :
- left / right / bottom / top: Ces paramètres représentent les coordonnées de l'écran, sur l'axe vertical et horizontal.
- zNear / zFar: Ces deux paramètres sont les limites en profondeur de la perspective. Peu utile pour la rendu en 2D.
La pile de matrice de modèle
Le but de cette pile de matrice est de positionner les entités (objets géométriques, lumières, la caméra...) dans une scène. Les principaux méthodes de transformations sont invoqués dans cette matrice afin d'éditer le repère, s'y "déplacer", et lui ajouter les objets à la position que nous souhaitons. Ces entités peuvent être aussi modifiées par les méthodes de transformations: pour les agrandir, y appliquer une rotation, etc...